Tutorial
Gain for Compressed Amplifiers
There is growing interest in operating amplifiers into compression to achieve higher power-conversion efficiencies. It becomes constructive then to revisit the concept of amplifier gain, because when an amplifier operates in compression the general assumption that the output signal is directly proportional to the input signal is no longer valid. Two approaches to the concept of gain, differential (small-signal) and ratiometric (large-signal) are examined. These are shown to match at small-signal levels while diverging as amplifier compression increases. Differential gain characteristics relate to output waveform distortion, and hence to amplifier linearizer design. Power gain, as used in RF engineering standard practice, is shown to be a ratiometric measure.
Earl McCune
Tropian Inc.
Cupertino, CA
Differential gain is a well known small-signal characteristic of an amplifier, defined as the slope of the amplifier voltage transfer function

However, real amplifiers exhibit output compression when the output signal falls behind the level predicted by Equation 1a and eventually hits a maximum level y = ymax (output clipping). Ignoring memory effects (generally dangerous for amplifier design1,2 but acceptable for the present purposes) this compression phenomenon can be described mathematically with a polynomial model (valid only below clipping) as

where
a0 = DC offset
a1 = linear differential gain (g from Equation 1a)
D = distorting term 
xc is defined as the input level at the onset of output clipping: y(xc ) = ymax . the differential gain for the amplifier modeled by Equation 2 is then

When the amplifier reaches and enters the clipping region (x > xc ), the differential gain (Equation 1b) is zero. This means that changes in the input signal no longer effect changes in the output signal. In keeping with convention, all use of the term gain for the remainder of this article is understood to refer to differential gain.

Fig. 1 Linear, linearized and output clipping modes of an amplifier.

Fig. 2 Linear and compressed amplifier characteristics with corresponding normalized compressed gain.
Plots of Equations 1a and 2 are shown in Figure 1 , where the polynomial of Equation 2 is truncated to the seventh-order. It compares the polynomial amplifier model with the ideal amplifier. Regions where the linear model is valid, and where clipping occurs, are shown. Also shown is a region where linearizer techniques can be applied to extend the linear amplifier operation. Figure 2 adds a plot of Equation 3, showing the normalized gain as it drops from its nominal value in the linear region to zero when the amplifier begins clipping.
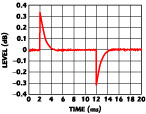
Fig. 3 Operation of a clamped linear amplifier with sinusoidal drive.
It is also important not to confuse output waveform clipping (also referred to as output waveform clamping) with output power saturation. These are very different phenomena, as shown in Figure 3 . For a sinusoidal input signal, the output signal is also sinusoidal while the amplifier is operating linearly. With the onset of clipping, the output waveform begins to be distorted. As the input signal is increased further, the output waveform distortion also increases as the output signal progresses toward a square wave. For equal peak amplitudes, there is 4/π or approximately 2.1 dB more power in a square wave than a sine wave. Output power saturation does not occur until the output waveform becomes a square wave, which occurs in the limit of infinite input signal, as shown in Figure 4 .

Fig. 4 Output power compression in a linear amplifier.
A primary intent for an amplifier is for the output signal to be larger than the input signal, which is likely to be true even when the amplifier output is clipping (but may not be true when there is output power saturation). This leads to a different concept of gain, based not on a differential model but on a ratio model called the input-output ratio (IOR), shown as

where vout corresponds to y, and vin corresponds to x, in Equation 1a. Equations 3 and 4 clearly agree only for very small input signals (x near 0). In the absence of compression, where Equation 1a applies, there is no difference between small-signal and large-signal performance, and Equation 4 also describes the amplifier gain. It is a common assumption in the literature to ignore compression and to treat Equation 4 as an expression for gain. However, it is important to remember that, in general, amplifier gain is not the same as IOR, particularly for large-signal operation. A comparison of Equations 3 and 4 for the given seventh-order amplifier model is shown in Figure 5 .

Fig. 5 Comparison between the amplifier gain and IOR.
On first glance, looking only at the IOR curve, one might imply that the amplifier is quite linear since the normalized IOR curve is rather flat near unity for a large input signal range. However, only the gain curve (Equation 3) represents the amplifier performance with regard to waveform fidelity, not the IOR. These two curves, after all, are describing the same amplifier.
Standard RF engineering practice is to describe the power gain of a stage as the difference in the decibel power measured at the output and input of the stage. Using capital letters for decibel and lower case for linear measures of signal power this becomes

For equal input and output impedances this can be rewritten as
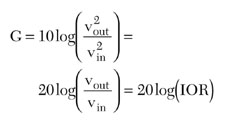
Thus, power gain is related to IOR, and not to linear gain except at small-signal operation, which, for clipped or saturated operation, is clearly not the case.
References
1. S.C. Cripps, RF Power Amplifiers for Wireless Communications , Artech House Inc., Norwood, MA 1999.
2. S.A. Maas, Nonlinear Microwave Circuits , IEEE Press, New York, NY 1997.
Earl McCune received his BSEE/CS degree from the University of California at Berkeley, his MSEE degree from Stanford University and his PhD degree from the University of California at Davis. He has over 25 years of experience in RF circuit and systems engineering, and has worked for Proxim, Digital RF Solutions, Cushman, Watkins-Johnson and Hewlett-Packard (now Agilent). He is a co-founder of Tropian Inc., and serves as its CTO. He holds over 15 patents in the US and worldwide.
