Technical Feature
Simulating Multi-finger Power HBTs
A new model of multi-finger heterojunction bipolar transistors (HBT) is presented to analyze and predict current collapse, bias dependence and output power. The simulation of multi-finger HBTs has proven to be very challenging in both computer-aided design and electromagnetic (EM) simulation. However, by taking the biasing scheme into consideration, a successful simulation can be performed that enables the analysis of temperature and bias variations in each finger. This analysis includes self-heating, coupled thermal effects in multiple ports, current collapse and output power reduction. By incorporating multiple unit finger HBT models with a multi-port thermal network, a model is developed that enables thermal effects with DC, small-signal and large-signal simulations to be modeled in a circuit simulator.
Yu Zhu, Jason Gerber and Qian Cai
Ansoft Corp.
Pittsburgh, PA
HBTs have earned a reputation in high frequency circuit design for offering outstanding power efficiency and high linearity in applications such as power amplifiers, where they enable longer battery life and better signal characteristics in wireless devices. In addition, some versions of HBTs also provide the high performance characteristics suitable for use in high data rate fiber-optic devices. As a result, they have become attractive for use in microwave and millimeter-wave applications.
Unfortunately, thermal effects can significantly affect HBT performance, particularly with multi-finger HBTs where self-heating in a unit emitter finger and the thermal coupling among the fingers can lead to non-uniform temperature distributions. An accurate simulation is required to assist in their design and thus reduce time to market. One approach is to use electro-thermal models where each finger is represented by a unit finger HBT model, and all fingers are thermally coupled through a thermal equivalent circuit or thermal network.1,2
An overlooked area of concern with this approach is the bias scheme. There is a non-uniform temperature distribution among the fingers (each finger exhibits a different bias point for the same external bias source) due to self-heating. The level of inconsistency is strongly dependent on the bias scheme, so it is an important consideration in successful simulation.
Building a New Model
It is possible to incorporate the temperature and bias dependency of power HBTs in a model by using a thermal network to represent the self-heating and thermal coupling. Such an improved multi-finger HBT model was developed and implemented in a nonlinear circuit simulator, Serenade, from Ansoft Corp.
When increasing the collector-emitter voltage of a unit finger HBT, an increase (decrease) in collector current can be observed when the base is biased with a voltage (current) source.3 Since a current source can be equivalently replaced by a voltage source with a series resistance, the bias behavior of a self-heating HBT can be summarized as follows: When the base of a unit finger HBT is biased with a voltage source with a series resistance Rb , the collector current at a given Vce changes continuously with Rb and reaches its maximum (minimum) when Rb = 0 (Rb ® ∞).
With a constant voltage base bias, a decrease in the turn-on voltage of the emitter junction causes an increase in collector current. In addition, when using a constant current base bias, an increase in the reverse hole injection from the base to emitter causes a decrease in collector current. By accurately describing these two effects, a true model can be constructed.
For instance, in an example simulation, a modified Gummel-Poon model for a self-heating HBT was used to represent a unit finger HBT. The decrease in the emitter junction turn-on voltage can be accounted for by adding a temperature-dependent base voltage source
Vth = aDT (1)
where
a = thermal electric feedback coefficient
DT = temperature increase
The increase in the reverse hole current component from the base to emitter is realized by adding a diode between the base and emitter nodes, which is correlated with the electron current component.
Ip = CIc exp( DE/kT) (2)
where
DE = effective difference in energy barrier height seen by electrons and holes
C = hole and electron current ratio at emitter junction for DE=0
The Ic -Vce characteristics of a unit HBT with different Rb are calculated and shown in Figure 1 . The Ic -Vce characteristics change gradually from a constant V base bias to a constant I with increasing base series resistance. This figure demonstrates how the unit finger HBT model exhibits a bias scheme dependence. It is useful to note that the Vce dependence of Ic (and thus the temperature dependence of Ic ) can be effectively reduced with a base series resistance in the range of 100 to 400 W under constant Vbe .
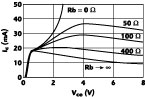
Fig. 1 Calculated Ic vs. Vce of a unit finger HBT with different base series resistances.
Modeling the Thermal Network
One way to represent the thermal resistance of an n-finger HBT is by an n x n matrix. In this matrix, the diagonal values represent the self-heating of each finger, and the off-diagonal values represent the thermal coupling among the fingers. In such a matrix, the values are typically obtained using a thermal solver. This approach is limited because available thermal field solvers provide only the field solution, and multiple separate calculations must be performed for extracting the thermal resistance matrix. Therefore, in this example, the Ansoft SI3D electric field solver was used instead, because it solves the electric field solution and can provide an equivalent resistance matrix with a single calculation. By substituting thermal conductivity for electrical conductivity, for instance, the equivalent resistance matrix generated is identical to the thermal resistance matrix.
As an example, an extraction was performed on an HBT with two fingers of 2 x 50 mm2 . The dependence of the thermal coupling resistance (off-diagonal value) on the distance between the fingers, as calculated by the electric field solver, is shown in Figure 2 . Thermal field calculations for the same HBT are also plotted, with their close correlation demonstrating the accuracy of using the electric field solver.
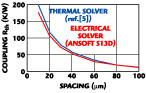
Fig. 2 Extracted coupling thermal resistance using thermal and electrical solvers.
From a larger perspective, the thermal resistance matrix contains the Z-parameters of the thermal network. Therefore, the thermal equivalent circuit in this approach is represented by a multi-port black-box component (which is available in most circuit simulators) with the thermal resistance matrix given as Z-parameters. Thus, the construction of a schematic form of the thermal equivalent circuit, which becomes topologically complex with increasing numbers of fingers, can be avoided.

Fig. 3 Electro-thermal model of multi-finger HBT; the node voltage T1 to T5 represents the temperature rise at each finger.
Using the Model
The example multi-finger HBT model (implemented in the nonlinear circuit simulator) is shown in Figure 3 . The thermal node of each HBT finger is connected to a port of the thermal network. The electric current fed into the thermal network represents the power dissipated in each HBT finger, while the voltage at the port of the thermal network equals the temperature increase in each HBT finger. The thermal capacitance is represented by the capacitors in parallel with the thermal network.

Fig. 4 Calculated collector current in a five-finger HBT with constant base current.
Each unit finger HBT model has the same Gummel-Poon parameters, and the thermal resistance matrix of a five-finger HBT was extracted and used as the Z-parameters of the thermal network. The unit finger size is 2 x 10 mm2 , the finger spacing is 20 mm and the thickness of the GaAs substrate is 100 mm. The calculated Ic -Vce behavior of the five-finger HBT under constant base current is shown in Figure 4 . The current collapse, a unique behavior of multi-finger HBT, is demonstrated by the increasing Vce . Figure 5 shows the calculated individual collector currents in each finger and the total current of the five-finger HBT. It can be seen that current collapse is triggered by the non-uniform current distribution among the fingers, and one finger conducts almost all the current when Vce > 6 V.5
The current collapse can be prevented when a base series (ballasting) resistance is inserted for each unit finger under constant Ib .4 This model also reproduces the absence of current collapse. For example, with the insertion of a series resistance in the base, the base currents fed to each finger of a multi-finger HBT are somewhat equalized, which reduces the current non-uniformity and prevents current collapse.

Fig. 5 Calculated individual collector current in each finger and total current and total current of a five-finger HBT with Ib = 1.0 mA.
The study of bias dependence of a unit finger HBT model can lead to the analysis of the bias dependence in a multi-finger HBT model. When a base series resistor is inserted into the model for each finger, the Ic -Vce behavior of the multi-finger HBT under constant Vbe can be calculated (Figure 6 ). Interestingly, besides removing the current collapse, the dependence of Ic on Vce is also reduced. (For the multi-finger HBT under constant Vbe , the absence of current collapse is due to the reduction of temperature dependence of Ic in each finger.)

Fig. 6 Calculated Ic vs. Vce characteristics of a five-finger HBT with constant Ib and a base ballast resistance Rb = 100 W inserted in each finger.
The output power characteristics can also be calculated for the five-finger HBT under two biases: A - Ib = 1.0 mA, B - Vbe = 1.46 V, Rb = 250 W. Figure 7 shows the power behavior at 2 GHz of the multi-finger HBT model. At the 1 dB gain compression point, the output under bias B is approximately 2 dB better than that under bias A. Higher power output can thus be expected for the HBT under bias B, and the decrease in the Pout under bias A is most likely due to current collapse.

Fig. 7 Calculated output power vs. input power at 2 GHz for a five-finger HBT under two different biases.
The fundamental and third-order intermodulation power (IMD3) calculated under bias A and B are shown in Figure 8 , with input signals at 1.959 and 1.961 GHz. In the linear region, IMD3 under bias B is approximately 6 dB better than that under bias A, and the intercept points (IP3) under bias A and B are +27.5 and +29.5 dBm, respectively. The simulations clearly demonstrate that the bias-dependent device model is an important factor, especially in a multi-finger HBT circuit design.
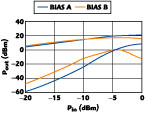
Fig. 8 Calculated fundamental and IMD3 behavior for the two different biases.
Conclusion
A multi-finger power HBT model, based on bias-dependent unit finger HBT models and a thermal network representing self-heating and thermal coupling effects, has been developed and implemented into a nonlinear circuit simulator. The simulation performed on a five-finger HBT also reproduces current collapse related behaviors. This model can be used in a circuit simulator in order to investigate the influence of device structure and the impact of bias scheme on the performance of multi-finger HBTs, serving as a practical tool for both device and circuit design.
References
1. C.M. Snowden, "Large-signal Microwave Characterization of AlGaAs/GaAs HBTs Based on a Physics-based Electro-thermal Model," IEEE Transactions on Microwave Theory and Techniques , Vol. MTT-45, No. 1, January 1997, pp. 58-71.
2. A. Marty, et al., "A Self-consistent DC-AC Two-dimensional Electro-thermal Model for GaAlAs/GaAs Microwave Power HBT's," IEEE Transactions on Electron Devices , Vol. 40, No. 7, July 1993, pp. 1202-1210.
3. Y. Zhu, et al., "Compensation of Self-heating Effect in DC and Pulse Characteristics of HBTs," 1999 IEEE MTT-S International Microwave Symposium Digest , Vol. 2, June 1999, pp. 431-434.
4. W. Liu, A. Khatibzadeh, J. Sweder and H. Chau, "The Use of Base Ballasting to Prevent the Collapse of Current Gain in AlGaAs/GaAs Heterojunction Bipolar Transistors," IEEE Transactions on Electron Devices , Vol. 43, No. 2, February 1996, pp. 245-251.
5. W. Liu, "Thermal Coupling in 2-finger Heterojunction Bipolar Transistors," IEEE Transactions on Electron Devices , Vol. 42, No. 6, June 1995, pp. 1033-1038.
Yu Zhu received his BS and MS degrees in applied physics from Shanghai Jiao Tong University, Shanghai, China, and his PhD degree in electrical engineering from Kyoto University, Kyoto, Japan. His doctoral research covered epitaxial growth and characterization of III-V semiconductors, modeling and fabrication of optoelectrical integrated devices. From 1992 to 2000, he was with the Central Research Laboratories, Sharp Corp., Nara, Japan, working on the modeling and characterization of HEMTs and HBTs, and the design of monolithic microwave integrated circuits (MMICs). In 2000, he joined Ansoft Corp., Elmwood Park, NJ. His current research focuses on the active devices modeling for microwave circuit simulation.
Jason Gerber received his BSEE from Drexel University in 1986 and his MSEE from the University of Massachusetts in 1989. He joined Compact Software (now Ansoft Corp.) in 1988, developing nonlinear harmonic-balance simulation tools and transistor parameter extraction tools. He is presently a vice president of R&D for the Serenade circuit simulation product. His interests are in the research and development of high frequency circuit analysis, microwave transistor characterization and the development of integrated design tools.
Qian Cai received his PhD degree from McMaster University, Hamilton, Ontario, Canada, in 1992. He is currently a senior research engineer for Ansoft Corp., where he is working on various projects of circuit CAD including device physics and modeling, circuit simulation and optimization, statistical modeling and design, sensitivity analysis and yield optimization. He is a senior member of IEEE.
