Externally Induced VCO Phase Noise

Tutorial

Externally Induced VCO Phase Noise

This article describes the degradation of VCO phase noise due to noise on tuning and supply lines, particularly from tuning source resistance and supply voltage regulators.

Dennis Colin
Micronetics Wireless
Hudson, NH

VCOs, especially low noise wideband units, are extremely sensitive voltage-to-frequency converters, and are therefore very sensitive to noise on the tuning and supply sources. Even the thermal noise of a 50 W tune driver output resistance can degrade the expected phase noise performance. In this article, calculations are compared with experimental results; also discussed are degradation-minimizing methods.

Theory

Phase noise is generated in an otherwise noiseless VCO by frequency modulation (FM) of the oscillator signal (f_o ) by the noise present (V_n ) at the tuning or power supply input, as shown in Figure 1 . In the latter case, supply-pushing is the modulation mechanism. Except in extreme cases, the modulation index (M) is much less than unity: M = D f/f_MOD where Df is the frequency deviation and f_MOD is the modulating frequency.

Fig.1 Generation of externally induced phase noise.

Bessel functions are used to calculate each FM spectrum component amplitude as a ratio of its peak sine wave voltage to that of the unmodulated carrier, all as a function of M. Bessel functions apply only to sinusoidal (single frequency) modulating signals of frequency f_MOD , and Df is the peak deviation. For a VCO modulated by a sine wave, Df is the peak voltage (not RMS) multiplied by the tuning sensitivity K_v .

Noise (or any other multi-tone modulating signal) cannot be represented by Bessel functions; for high values of M, the FM spectrum is very complex. But with M lower than approximately 0.1 (the noise in VCOs is usually much lower; typically M is less than 10^-4 ), nearly all the modulation spectrum is in the first-order FM sideband pair, each of which is a nearly ideal frequency translation (f_o ± f_MOD ) of the modulation signal's multiple (or noise) components, with an added slope of -20 dB/decade because carrier phase excursion, not frequency, determines the sideband amplitude.

Thus, Bessel functions can be used to adequately calculate a VCO phase noise due to external noise modulating the tuning and supply inputs. But the question is, will the RMS value of this noise work correctly? The answer is no. With sinusoidal FM, the peak voltage is specified in Bessel functions. Noise has no defined peak; the RMS value is therefore used universally.

Therefore, one can simply calculate this value with a sine wave, using the RMS value, which results in sideband amplitudes 3 dB lower than their correct value (for M << 1), and this value is applied to noise modulation by adding 3 dB to the RMS voltage-based calculations. This method works, because at very low M values, the dominant first-order sideband amplitudes are almost linearly proportional to the modulating signal amplitude, as discussed previously. The sideband amplitudes, as a fraction of that of the carrier (f_o ), are approximately represented by

A = Df/2f_MOD

where

A = V_sideband /V_carrier
Df = the peak frequency deviation.

Therefore, if Df is expressed as an RMS deviation, as one must with noise, then A = Df_RMS /√2 f_MOD . As required, this is corrected for the 3 dB sine wave peak to RMS ratio considered in the Bessel function utilization described. The sideband amplitude expressed in dBc is then 20 log (Df_RMS /√2 f_MOD ).

In a VCO of tuning slope Kv (Hz/V), whose input is a noise of density N (V/√Hz), any 1 Hz bandwidth segment centered about an arbitrary frequency f_MOD will produce a 1 Hz wide phase noise segment at an offset frequency f_os = f_MOD , and its amplitude in dBc/Hz is 20 log (D f_RMS / √2 f_MOD ) since a 1 Hz bandwidth noise segment was used. Since Df_RMS due to that 1 Hz segment is NKv (RMS Hz), and f_MOD = f_os , an equation can be written for externally induced phase noise, hereby referred to as £_(fos)E (dBc/Hz) = 20 log (NKv/√2f_os ).

Fig. 2 Test setup.

Demonstration of VCO Phase Noise Degradation

Figure 2 shows the test setup. A 1250 to 2550 MHz VCO was used at 1875 MHz, where the tuning rate is 81 MHz/V, and the 100 kHz phase noise is -120 dBc/Hz (Figure 3 ) when using low noise shielded battery supplies for both tuning and bias supply voltages. In addition to providing isolation from AC equipment grounds, these supplies have a noise density less than 0.5 nV/√Hz (open-circuit thermal noise of a 15 W resistor, the measurement limit here) at frequencies above 100 Hz.

Fig. 3 SSB phase noise of a 1875 MHz VCO, with battery tuning and bias supplies (R_T <1 W ).

In the first test, a tuning source resistor (Rt) of 50 W or 1000 W was inserted between the tuning supply and the VCO. Figures 4 and 5 show their effect on phase noise; the degradation is 1.2 dB with R_t = 50 W and 8.6 dB with R_t = 1000 W .

Fig. 4 SSB phase noise of a 1875 MHz VCO, with battery sources for R_T = 50 W .

Fig. 5 SSB phase noise of a 1875 MHz VCO, with battery sources for R_T = 1000 W .

In the second test (Figure 6 ), the VCO +12 V bias was supplied by an LM317T regulator, whose measured noise density at 100 kHz is 2.07 mV/√Hz (67 dB higher than the open-circuit thermal noise of a 50 W resistor). Figure 7 shows its effect; the VCO's noise at 100 kHz is degraded by 24.6 dB. Note that this VCO has a relatively low supply-pushing value of 1.1 MHz/V; a VCO with 10 MHz/V pushing (and the same 81 MHz/V tuning rate and -120 dBc/Hz phase noise at 100 kHz) would have its noise degraded by approximately 44 dB.

Fig. 6 Supply regulator for regulator noise test.

Fig. 7 SSB phase noise of a 1875 MHz VCO, with battery tune source and different 12 V supplies.

This regulator's noise can be reduced by the addition of the capacitor Ca. 100 mF lowered the noise degradation from 24.6 to 5.3 dB (Figure 8 ). However, the regulator's manufacturer cautions about using large values of C_a .

Fig. 8 SSB phase noise of a 1875 MHz VCO, with battery tune sources and different 12 V supplies showing the effect of C_a = 100 m F.

Notes on the RDL NTS-1000 A Phase Noise Analyzer

An RDL DCR-2500 downconverter was used (2560 MHz LO, 1800 to 2500 MHz input range) between the VCO and the NTS-1000 A mainframe; the frequency received by the mainframe was approximately 685 MHz. The analyzer is very repeatable; the same VCO sample gave results within 0.5 dB, tested twice a year apart.

A tuning voltage output is provided. While this is stated to be very clean, it produced the upper curve in Figure 9 . Before concluding that the tuning output is defective, however, consider that it comes from one large AC-operated box (mainframe), while the VCO RF output plugs into another one (downconverter), in a laboratory full of all the usual equipment and lights and adjacent to a semiconductor fabrication laboratory with all its arc welding equipment. While the portion of the curve below 10 kHz offset shows a distinct -20 dB/decade slope (consistent with the tuning source resistance noise; the RDL manual states a 1000 W output impedance), the extreme noise peaks above 10 kHz may not seem so extreme after electromagnetic interference (EMI) sensitivity considerations.

Fig. 9 SSB phase noise of a 1875 MHz VCO, with different tuning supplies.

EMI Sensitivity of Wideband Low Noise VCOs

Note that all plots using the 1250 to 2550 MHz VCO have a spike at approximately 120 kHz of about -93 dBc/Hz amplitude (plus a lower-level second harmonic). This is present almost constantly during normal laboratory hours; being so constant and narrow band this EMI is easily ignored.

However, it is interesting to calculate the voltage received by the VCO tuning port required to produce the observed -93 dBc/Hz level. First, however, it is necessary to correct this for the analyzer's resolution bandwidth, which increases with each offset frequency decade. Calibrated for noise, a single-frequency signal's indicated amplitude in dBc/Hz must be corrected; RDL states that for 100,001 Hz to 1 MHz offsets, 32.9 dB must be added to the indicated dBc/Hz value to obtain the actual level in dBc.

Thus, the 120 kHz spur level is actually -60 dBc. The VCO, with K_v = 81 MHz/V, would then need a tuning port signal of only 3 mV to produce the observed 120 kHz level. If the interference source were, for example, a fluorescent light switching ballast supplying 400 V of 120 kHz lighting power (scattered all over the lab ceiling), this would have to be attenuated by 162 dB to result in 3 mV received by the VCO. Expressed another way, only 6 x 10^-17 of the interfering power source would have to be intercepted.

This simple example is imprecise due to several assumptions, but with even a ballpark figure of 160 dB path-length and shielding attenuation causing very observable interference, the need for the utmost care in phase (or other) noise measurements is well demonstrated.

Calculated Noise Degradation Due to Tuning Source Resistance

For the first example, R_t = 50 W and the open-circuit noise density (N) = 0.9 nV/√Hz, K_v = 81 MHz/V.

The externally induced phase noise is

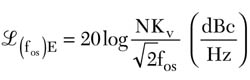
Adding this to the VCO's own phase noise of -120.0 dBc/Hz,

Total noise (£_T ) = 10 log [antilog(-125.8/10) + antilog (-120.0/10)]
Calculated £_T = -119.0 dBc/Hz
Measured £_T = -118.8 dBc/Hz

Difference:

D£_T (measured - calculated) = 0.2 dB

For the case of Rt = 1000 W, the open-circuit noise density N = 4.02 nV/√Hz.

£_(fos)E = -112.7 dBc/Hz @ 100 kHz
Calculated £_T = -112.0 dBc/Hz
Measured £_T = -111.4 dBc/Hz
D£_T = 0.6 dB

Calculated Noise Degradation Due to Regulator Noise (C_a = 0)

The LM317 12 V regulator noise (with VCO load) was measured in two ways. First, the output was AC coupled to a low frequency LNA, (LFLNA) with 60 dB gain and an input noise voltage density of 1.54 nV/√Hz and connected to an HP8566B spectrum analyzer. The noise output was flat to ±0.5 dB from 100 Hz to 100 kHz (the upper limit of the LFLNA flat response). The regulator output noise density was calculated to be 2.07 mV/√Hz.

Second, filters within the LFNA were switched in, with a -3 dB bandwidth of 1.0 to 16.2 kHz. The measured equivalent noise bandwidth is 24.1 kHz. Measuring the LFLNA noise output (312 mV) on a Fluke 8010A, true-RMS meter, resulted in a calculated regulator noise density of 2.01 mV/√Hz, within 0.26 dB of the spectrum analyzer result.

The National Semiconductor data sheet for the LM317 regulator states a typical RMS noise output of 0.003 percent of the DC output (12 V here) over a 10 Hz to 10 kHz bandwidth. The resulting 360 mV noise over this bandwidth yields a noise density (already determined to be very flat) of 3.6 mV/√Hz, conservatively rated relative to the previously measured noise levels.

The VCO supply-pushing figure was previously determined to be 0.7 MHz/V in a static DC test. However, when changing the supply voltage (V_s ), the VCO dissipation heating changes the frequency through its temperature coefficient. As it turned out, the latter's negative value (approximately -0.2 MHz/°C) partially cancelled the (positive) supply-pushing effect. Therefore, pushing was measured dynamically by superimposing an AC signal (at 120 Hz and 100 kHz) on the 12 V DC supply; two different methods were used:

Fig. 10 VCO output with the power supply modulated by a 100 kHz signal.

First, with a 1.038 V peak-to-peak 120 Hz square wave added to the 12 V DC, the VCO output spectrum showed the expected two peaks, spaced apart by 1.15 MHz. This yields a pushing value of 1.108 MHz/V. The 120 Hz supply switching rate is much too fast to allow thermal effects to interfere. Secondly, the supply modulation used was a sine wave at 100 kHz (still well within the VCO supply modulation bandwidth of 7.9 MHz). The 100 kHz modulation amplitude was adjusted to produce an FM spectrum (Figure 10 ) whose first-order sideband amplitudes equaled that of the (reduced by modulation) carrier (f_o ).

This occurs repeatedly with increasing modulation index

M = Df_peak /f_MOD

the lowest such value of M is 1.435. At M = 1.435, the first five Bessel functions (mathematically derived voltage ratios relative to the unmodulated carrier) are

J_o = 0.5475 = -5.23 dBc (carrier);
J₁ = 0.5475 = -5.23 dBc (first-order sidebands);
J₂ = 0.2161 = -13.3 dBc;
J₃ = 0.0542 = -25.3 dBc;
J₄ = 0.0100 = -40.0 dBc.

As can be seen from the spectrum plot, the measured component amplitudes are very close to the Bessel function values.

Since the VCO supply is being modulated, there will also be amplitude modulation. This VCO has a power-pushing value of 1.0 dB/supply volt. Thus, with 259 mV peak-to-peak (100 kHz) applied, the amplitude change is 0.26 dB peak-to-peak, or ±0.13 dB, a voltage modulation of about ±1.5 percent. With 100 percent AM (±100 percent voltage modulation) the two AM sidebands are each -6 dBc, thus, ±1.5 percent (1.5 percent AM) has a sideband level of -42.5 dBc. This is 37.5 dB below the same frequency first-order FM sidebands, causing a maximum error of ±0.12 dB.

With M established to be very close to 1.435, the VCO frequency deviation Df_peak = Mf_MOD = 143.5 kHz or 287 kHz peak-to-peak. The corresponding VCO supply modulation amplitude was 259 mV peak-to-peak. The resulting pushing value is 1.108 MHz/V, within 0.001 MHz/V of the 120 Hz square wave test result.

With both the regulator noise and VCO supply-pushing values believed to be accurately determined, the externally-induced VCO phase noise can be calculated as

£_(fos)E = -95.8 dBc/Hz

Calculated Total noise
£_T = -95.8 dBc/Hz

(within 0.1 dB of the externally-induced noise because this is 24 dB above the VCO's own noise)

Measured £_T = -95.4 dBc/Hz
D£_T = 0.4 dB.

A Different VCO

Another wideband VCO, but at a much lower frequency (90 to 140 MHz), is used at 93 MHz. Its pertinent specifications are K_v = 2.61 MHz/V, phase noise = -123.2 dBc at 10 kHz and -143.8 dBc at 100 kHz (Figure 11 ).

Fig. 11 SSB phase noise of a 93 MHz VCO, with battery tuning and bias supplies and R_T < 1 W .

Fig. 12 SSB phase noise of a 93 MHz VCO, with battery sources and R_T = 1000 W .

Figure 12 shows the phase noise increase when R_t = 1000 W. Increased by 3.9 dB, the phase noise at 10 kHz is 119.3 dBc/Hz.

Calculated externally induced noise =
£_(fos)E = -122.6 dBc/Hz
Calculated £_T = -119.9 dBc/Hz
Measured £_T = -119.3 dBc/Hz
D£_T = 0.6 dB

All four tests are summarized in Table 1 .

Relative VCO Tuning Port Noise Sensitivity Figures

The effective tuning noise (ETN) can be defined as the noise density fed to the tuning port of an ideal (intrinsically noiseless) but otherwise identical VCO that would produce the same phase noise (at a given offset frequency) as the intrinsic noise of the actual VCO being considered.

This noise density fed to the actual VCO would increase its phase noise by 3 dB.

Effective tuning resistance (ETR) is a hypothetical resistance value whose thermal noise voltage, when presented to the tuning port of an ideal (noiseless) VCO, would produce the same phase noise that the actual VCO has intrinsically.

Theoretically, a resistance of this value appearing between the tuning port and ground would increase the VCO phase noise by 3 dB.

Example 1

£ = -120 dB/Hz
f_os = 100 kHz
K_v = 81 MHz/V
ETN = 1.75 nV/√Hz
ETR = 188 W

Example 2

£ = -144 dB/Hz
f_os = 100 kHz
K_v = 2.61 MHz/V
ETN = 3.42 nV/√Hz
ETR = 721 W

Example 3

£ = -123 dB/Hz
f_os = 10 kHz
K_v = 2.61 MHz/V
ETN = 3.84 nV/√Hz
ETR = 908 W

ETN and ETR can be viewed as figures of merit analogous to the noise figure of an amplifier. Actually, a VCO is a kind of amplifier (a parametric amplifier with frequency being the output parameter). Like a noise figure, a lower value of ETN (thus also ETR) signifies the ability to detect a lower signal (tuning voltage change) with respect to noise present at its input.

In open-loop (free-running) VCO applications, the output noise is the figure of merit, not the ETN. But in a loop, within its bandwidth (where much of the VCO noise is cancelled), the equivalent input noise is the limiting factor: by analogy, consider an op-amp with its usual large amount of negative feedback - the input-referred noise times the closed loop gain determines the output noise.

So it is with a phase-locked loop (PLL); the ETN figure is the VCO's equivalent input noise.

But in free-running VCOs, and PLLs near and above the loop bandwidth, ETN and ETR are measures of the VCO's sensitivity to tuning input noise, expressed directly as a voltage or as a resistance whose thermal noise is equivalent.

Minimizing VCO Noise Degradation Tuning Supply

The loop filter in a PLL is often a passive RC low pass circuit between an op-amp and the VCO. Series resistors of approximately 1 kW are often used to allow small shunt capacitor values, and to minimize the AC load impedance driven by the op-amp. But as has been demonstrated, a 1000 W tuning source resistance will degrade a low noise wideband VCO's phase noise (by 8 dB with -120 dBc/Hz at 100 kHz and 81 MHz/V tuning rate for the VCO shown), which means the PLL's op-amp must have the lowest possible noise.

Of course, above the loop filter's rolloff frequency (where the loop stops canceling the VCO noise) the filter's shunt output capacitor starts presenting a lower impedance than the series resistor, thereby attenuating the latter's noise. However, the noise degradation will be significant near the filter rolloff frequency.

The solution is to use a low impedance filter; 50 W would (in the example presented) reduce the noise degradation to about 1 dB. Of course, there are two disadvantages: the op-amp must be able to drive a 50 W AC load (above the filter rolloff frequency) and large shunt capacitance values are required (3.2 mF for a 1 kHz rolloff).

Fig. 13 VCO supply filter.

Supply Voltage Source

As has been demonstrated, the first rule is "Don't use conventional regulators, such as the otherwise excellent LM317 types." It may be possible to find a low-enough-noise regulator, depending on the required noise performance and VCO parameters. But if not, a simple passive low pass filter, shown in Figure 13 , can attenuate the regulator noise sufficiently, where the filter -3 dB rolloff frequency is

Example

v_s = +5 V
i_s = 25 mA
regulator V_R = +7.5 V
R = 100 W
C = 47 mF

then

f_-3 = 50.8 Hz

Frequency (Hz)	Filter Attenuation* (dB)
100	7
1 k	26
10 k	46
100	k 66
*Neglecting series resistance of C

The drawbacks include a required higher voltage supply and the addition of two (inexpensive) components. One advantage (besides noise reduction) is that the series resistor tends to stabilize the VCO supply current; many VCOs will benefit from a flatter power output (with more constant current than a fixed-voltage supply will provide).

Load Pulling
A high SWR or unstable load not only causes VCO frequency pulling, but will also sometimes produce rapidly accelerated regions of the tuning curve (voltage-to-frequency transfer function). Tuned within such a region, the slope (K_v , in MHz/V) cannot only be high, but may actually become infinite with a "snap-like" discontinuity.

The problem is most serious with higher frequency VCOs with wideband, high K_v response and high power output (the latter requiring minimal internal output attenuation). For example, the model MW500-1089 VCO covers 4 to 6 GHz, has a maximum tuning slope of 180 MHz/V and uses only 2 dB of padding (to produce about +8 dBm). The frequency pulling is therefore high, about 70 MHz peak-to-peak with a 12 dB return loss load of any phase.

With this VCO, even a 12 dB mismatch can cause accelerated tuning regions if the load phase angle varies rapidly with frequency (caused, for example, by load resonances or long load path-lengths).

In addition, since an increased K_v often means higher phase noise, VCOs should have a stable, as low-as-possible SWR load impedance; the loop stability will also benefit.

Conclusion

Great care must be taken to prevent significant degradation of VCO phase noise, particularly for wideband units with low intrinsic noise. In one example shown, the thermal noise of a 50 W resistor (0.9 nV/√Hz at +25°C) increased the phase noise at 100 kHz by 1.2 dB, and the single-frequency spur level required at the tuning input to equal the 100 kHz phase noise level of -120 dBc/Hz is a mere 2.5 nV. Thus, the isolation required from a 100 V, 100 kHz switching power supply carrier is 212 dB, a power ratio of about 10^-21 .

While much less sensitive, the VCO supply driven from an LM317 regulator still added enough noise modulation to increase the VCO noise by 25 dB. Supply noise filtering is simple enough to implement, but the tuning input of a sensitive VCO requires the lowest noise, resistance and interference susceptibility possible, if state-of-the-art phase noise performance is to be achieved.

Reference
1. Bessel Functions, Reference Data for Radio Engineers, Fifth Edition, pp. 20-22, 45.

Dennis Colin received his BSEE degree from the University of Lowell and is currently the principal engineer (RF and analog design) of the Micronetics VCO Products Division in Hudson, NH. He has designed the three VCOs described along with others composing the MW500 series of 0.5" units covering 100 MHz to 7 GHz. His design experience comprises general RF/microwave components (particularly VVAs, RF log amps and high speed microwave radios) and analog instrumentation including RF device drivers, linearizers, voltage-controlled filters, switching power supplies and high quality audio components. He can be reached via e-mail at dcolin@micronetics.com or dcolin@worldpath.net.