Axial Ratio Measurements of Single Circularly Polarized Antennas

Technical Feature

Axial Ratio Measurements of Single Circularly Polarized Antennas

Robert Gunnels
Andrew Corp.
Orland Park, IL

The measurement of antenna axial ratios must be done properly if accurate results are to be obtained. When measuring on a terrestrial antenna test range, a straightforward approach is often used whereby the circularly polarized antenna under test (AUT) (also referred to as receiving antenna) is rotated about its electrical boresight while being illuminated by a linearly polarized wave. Sometimes it may be more convenient to keep the AUT fixed and instead rotate the source antenna polarization. In either case, the difference between the maximum and minimum received signal levels is a direct indication of the AUT's axial ratio. This, of course, is not practical or even possible when using a circularly polarized signal from a satellite to measure the axial ratio of a ground-based antenna.

Two novel and accurate techniques for determining the axial ratio of a circularly polarized antenna were presented nearly 20 years ago by Stutzman and Overstreet.¹ Their first method involves the use of two single or dual circularly polarized receiving antennas with measurements of maximum and minimum cross-polarization isolation values for each antenna when illuminated by a common circularly polarized illuminating wave. The resulting data is sufficient to allow for the calculation of the three axial ratios and differentiation between that for each antenna as well as for that of the incoming wave.

The second method requires only one receiving antenna, but it must be dual circularly polarized. The measurement of the maximum and minimum values of cross-polarization isolation, combined with the relative electrical phase, under those conditions, between the test antenna's co- and cross-polarized ports, provides the necessary information to determine the individual axial ratios of the antenna and illuminating wave.

Without the phase information, as required with the second technique, one can still calculate the two axial ratios, although there is an ambiguity as to which applies to the AUT and which is that of the incoming wave. A simple technique can be used to resolve this uncertainty. By slightly degrading the axial ratio of the AUT and again repeating the measurements of maximum and minimum cross-polarization isolation, this data can be considered to be that of a second, and necessarily different (in terms of axial ratio), antenna. Then by application of the procedure for two receiving antennas,¹ the aforementioned ambiguity is simply resolved while actually using only one receiving antenna. For testing with signals transmitted from a satellite, it is obviously quite impractical to make adjustments to the satellite antenna to change its axial ratio. However, this is not the case on terrestrial antenna test ranges. The axial ratio confusion can be resolved as well by making changes to the source antenna, instead of the AUT, and repeating the cross-polarization isolation measurements.

An adaptation of the Stutzman and Overstreet single receiving antenna method can be used to measure the axial ratio of one single circularly polarized antenna if a phase reference signal is available from a second receiving antenna, which can also be linearly polarized. For example, many modern antenna test ranges are equipped with multichannel receivers for the purpose of system phase locking and/or making ratio measurements so as to remove the effects of amplitude or phase variations in the incoming wave. The signal from a second "reference" antenna is often necessary and, therefore, probably already available. By noting the sense of antenna polarization and direction of AUT rotation, combined with the sense (positive or negative) of the AUT vs. reference antenna receive signal phase slope, the axial ratio ambiguity can again be resolved.

Take, for example, the case of an AUT configured to receive a right hand circularly polarized (RHCP) signal and illuminated by a left hand circularly polarized (LHCP) signal for the purpose of evaluating axial ratios. With the AUT rotated at various positions about its boresight axis, phasor representations of the combined cross-polar voltage for the AUT (V_xR ) and incoming wave (V_xW ) are shown in Figure 1 (V_xR < V_xW ).

First, the receive antenna and incoming wave cross-polar voltages add in phase, resulting in minimum isolation. In the successive examples, the AUT is rotated clockwise (as viewed from behind the AUT, opposite the direction of propagation of the incoming wave) through repeating conditions of maximum and minimum isolation. For the polarizations and direction of the receiving antenna rotation specified above, the cross-polar component V_xR becomes retarded in phase, whereas the component V_xW is advanced. Since, in this example, V_xW > V_xR , then the phase of their sum V_x advances in a positive sense as well. If, for the same antenna polarizations and rotation direction of the AUT, the phasor sum V_x retards in phase, then V_xW > V_xR . Therefore, based simply on the senses of the AUT and incoming wave's polarizations, and the direction of AUT rotation, knowledge of the sign of the resulting phase change of V_x is sufficient to determine which cross-polar contribution (V_xR or V_xW ) is greater. Thus, the axial ratios for the AUT (AR_R ) and illuminating wave (AR_W ) can be determined without ambiguity, using the calculations for the single antenna technique in Stutzman and Overstreet.

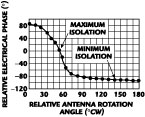
Figure 2 shows a plot of the relative electrical phase vs. relative antenna rotation angle for the polarization and cross-polar conditions indicated. In this case, the illuminating wave's axial ratio was intentionally degraded so that it was greater than that of the AUT. Note the positive slope of the phase response.

In Figure 3 the phase response is shown using the same antennas as before but with the transmitting antenna's axial ratio restored to a value better than and closer to that of the AUT. This results in a reversal of the phase slope sign.

It is understandable that for conditions where AR_R » AR_W and at maximum isolation, the magnitude of the phase slope will be the greatest. Conversely, at minimum isolation, under the same circumstances, the magnitude of the phase slope will be a minimum. If in fact AR_R = AR_W , then the phase response would simply be an up or down stair step function, depending on the polarization senses and the direction of antenna rotation. When AR_w > AR_R , there is a greater difference between the component axial ratios and, as a result, the magnitude of the phase slope does not change as much between conditions of maximum and minimum isolation. In contrast to the example above, where AR_R = AR_W , if AR_R = 1 and AR_W = ∞, then the phase slope would simply be a constant ±1 at any angle of antenna rotation.

It is important to note that to calculate the AUT's axial ratio from one arbitrary cross-polarization isolation value while assuming that AR_W = 1 can result in significant errors. If, for example, AR_R and AR_W are slightly greater than 1, and AR_R = AR_W , then depending on the angular relationship of their polarization ellipses, the measured cross-polarization isolation could range from approximately 6 dB worse to as much as infinitely better than that due to the axial ratio of the AUT alone. As an extreme case, imagine linearly polarized AUT and source antennas adjusted for a maximum cross-polarization isolation of 50 dB. If one were to incorrectly assume that AR_W = 1 and that the AUT is circularly polarized, then the AUT's voltage axial ratio, based on this level of cross-polarization isolation, would be calculated as 1.006, when in reality it is equal to 316! Simple rotation of either antenna would have immediately revealed the error.

When testing state-of-the-art, very low axial ratio circularly polarized antennas, it is unlikely that the source antenna will have a lower axial ratio by virtue of the fact that it cannot itself be better than the state-of-the-art. Furthermore, range ground or other sources of multipath reflections can also have an impact upon AR_W . Probably one of the most significant features of the Stutzman and Overstreet technique is its ability to suppress such adverse influences upon measurement accuracy.

Procedure for Measuring Axial Ratio of a Single Circularly Polarized Antenna with a Separate Phase Reference Antenna:

1. With the polarizations of the AUT (receiving) and transmitting antennas matched, store the receive data in the receiver/vector analyzer memory as a co-polarized ratio reference level (that is, A/R where A is the AUT receive signal and R is the reference antenna receive signal). Set the analyzer to display the measurement data normalized to the memory data (that is, A/R/M).

2. Switch the AUT or transmitting antenna's polarization. While measuring the relative phase between the AUT and a fixed reference receiving antenna (phase ratio measurement), rotate the AUT clockwise as viewed from the rear and note the sign of the change in phase.

3. If the AUT is RHCP, and the phase progression is positive (+), then AR_W > AR_R ; if negative (-), then AR_W < AR_R . If the AUT is LHCP, and the phase progression is positive (+), then AR_W < AR_R ; if negative (-), then AR_W > AR_R .

4. Rotate the AUT for minimum cross-polarization isolation and note the level (dB_MIN ).

5. Rotate the AUT for maximum cross-polarization isolation and note the level (dB_MAX ).

6. To inspire confidence in the measurements made in steps 4 and 5, note that between the positions of maximum and minimum isolation, the AUT should have been rotated 90° and the relative phase should have changed by ±90°.

7. Calculate the two axial ratios, AR_R and AR_W , with the following formulas, as from Stutzman and Overstreet:

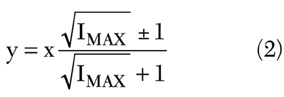
where

Since x > y, then x is equal to the greater of AR_W or AR_R , as determined in step 3, and y is equal to the lesser of the two.

Conclusion

A procedure for measuring the axial ratio of single circularly polarized antennas has been presented. The procedure expands on the work previously presented by Stutzman and Overstreet by including the use of a separate phase reference antenna and is particularly useful for measuring ground-based receiving antennas in satellite systems.

Reference
1. W.L. Stutzman and W.P. Overstreet, "Axial Ratio Measurements of Dual Circularly Polarized Antennas," Microwave Journal , Vol. 24, No. 10, October 1981, pp. 75-78.

Robert Gunnels is a research and development engineer with Andrew Corp., Orland Park, IL. He can be reached via e-mail at bob.gunnels@andrew.com.