RF peak power meters are the instruments of choice-simple and cost-effective-for measuring amplifier peak-to-average power ratios (PAPR) and assessing the effectiveness of PAPR reduction techniques.
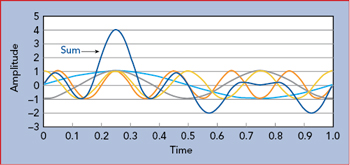
Figure 1 The sum of four sinusoidal subcarriers results in an occasional large peak.
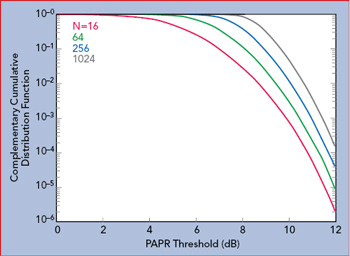
Figure 2 PAPR vs. number of OFDM subcarriers.
The ongoing, exponential growth in demand for mobile broadband services is no secret. To address this demand, enhanced mobile broadband (eMBB) is one of the cornerstones of the movement to 5G, and higher data rates are also a driver for improvements to military communications networks. To meet these needs, engineers are employing technologies that support high speed data transmission, mobility and more efficient use of the available spectrum and network resources. One of the staples across many communications systems is the use of orthogonal frequency division multiplexing (OFDM), which offers advantages in these areas. Applications include 4G (LTE), WLAN (IEEE 802.11a/ac/ax/g/n), digital radio, cable (DAB and DVB-C2), even broadband access over copper (ADSL).
In an OFDM signal, digital data is encoded on multiple frequencies or subcarriers. Each subcarrier is modulated at a low symbol rate with a conventional modulation scheme, such as quadrature amplitude modulation (QAM) or phase-shift keying, and occupies a sub-band of frequencies. Unlike other modulation schemes, such as frequency division multiplexing (FDM), the sub-bands can overlap to enable higher spectral efficiency, because each sub-band is orthogonal to the next. These factors enable OFDM to have lower susceptibility to narrowband co-channel interference, inter-symbol interference and fading caused by multipath propagation.1
One of the main disadvantages of OFDM is that the multiple carriers can add coherently and produce high PAPRs (see Figure 1). With the requirement for higher data rates, the number of subcarriers must increase to meet the demand, which will increase the PAPR. Figure 2 shows the relationship between PAPR and the number of subcarriers (N).2
IMPORTANCE OF PAPR
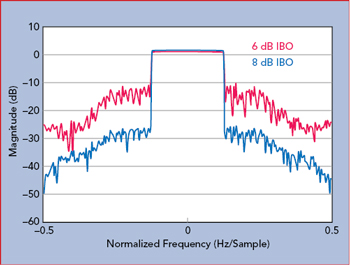
Figure 3 Spectral regrowth vs. IBO.
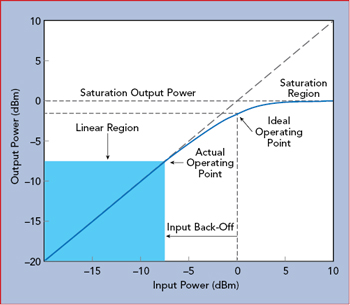
Figure 4 Input vs. output power for a typical SSPA.
High PAPRs cause a number of issues for amplifiers. If peak power is not properly considered, signals enter the nonlinear operating region of the amplifier, resulting in distortion and spectral spreading or regrowth. On the other hand, lowering the power, often referred to as input back-off (IBO), causes the amplifier to operate less efficiently. In Figure 3, the input signal to the amplifier is backed off by 6 and 8 dB; backing the signal off by only 6 dB results in higher spectral regrowth than if the signal is backed off by 8 dB. Spectral regrowth can cause interference among subcarriers, leading to an increase in bit error rate (BER); however, reducing the amplifier output power lowers the signal-to-noise ratio (SNR), which can also lead to an increase in BER. With a goal of higher data rates, poorer BER is counterproductive.
Efficiency is important in many applications. For mobile phones, the efficiency of its amplifiers drives battery life. For network operators, the efficiency of the base station impacts operating expenses. Amplifiers often operate most efficiently just into saturation. To illustrate this, an example of the relationship between input power, output power and efficiency for a solid-state power amplifier is shown in Figure 4.
The only way to minimize spectral regrowth and maintain high efficiency is to reduce PAPR. As a result, much research has explored techniques to lower PAPR in OFDM-based systems to reduce amplifier compression while minimizing the necessary IBO. Rahmatallah and Mohan2 provide an excellent review of the different techniques and trade-offs, summarized in Table 1. Clipping with filtering is most commonly used in commercial products because of its simplicity and ease of implementation.
PAPR is a singular, instantaneous value and does not provide a complete picture of signal behavior over time. As a result, many engineers utilize a complementary cumulative distribution function (CCDF) to monitor PAPR. When plotted, a CCDF curve displays the time a signal spends at or above a given power level (see Figure 5). For PAPR reduction investigations, the power level of interest is the signal’s average power, so the x-axis designates how much the peak power exceeds the average power in dB. The y-axis indicates the percent of time the signal spends at or above the difference in power specified by the x-axis. The point highlighted on the plot indicates the signal power exceeds the average power by at least 7.5 dB for 0.1 percent of the time. As a reference to compare amplifiers, engineers often plot the CCDF curve for a Gaussian noise signal. As the number of subcarriers increases in an OFDM signal, it approaches a Gaussian distribution.3 Figure 5 also shows the CCDF curve for a theoretical Gaussian noise signal. A signal with a CCDF higher than this reference is said to have gain expansion, and a signal with a lower CCDF is said to be in gain compression.
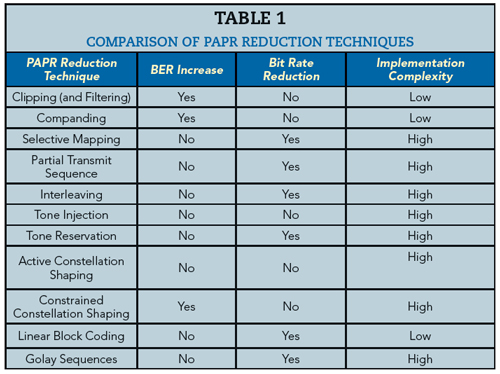
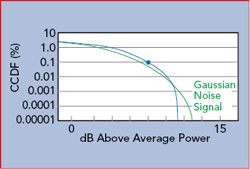
Figure 5 CCDF of an input signal vs. band-limited Gaussian reference.
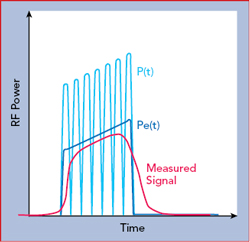
Figure 6 Insufficient video bandwidth distorts measurement of a pulsed signal.
MEASURING PAPR
An RF peak power meter with a diode-based sensor (or a USB RF peak power sensor which combines the power meter and sensor into one instrument) is the most widely used tool to measure peak power. Many peak power meters provide CCDF traces.
It is important to ensure that the power sensor is appropriate for the signal being measured. The ability of a diode sensor to accurately capture the peak envelope power requires it to respond at least as fast as the highest frequency component in the modulation envelope. A common measure to determine the ability of the sensor to respond fast enough is video bandwidth. Sensors use a low impedance load across the smoothing capacitors, to discharge them quickly when the RF amplitude drops. This, in combination with a very small smoothing capacitance, permits peak power sensors to achieve rise times in the nanosecond range and corresponding video bandwidths of tens or hundreds of MHz. A rule of thumb relationship between rise time and bandwidth is the bandwidth is approximately 0.35 divided by the rise time of the detection circuit. Figure 6 shows a pulsed RF signal, where P(t) is the instantaneous power and Pe(t) is the envelope power measured by a power meter. If the power meter has insufficient video bandwidth, the measured signal will “round” the corners of the signal and lag during the rise and fall times, resulting in an errant measurement, as illustrated in the figure.
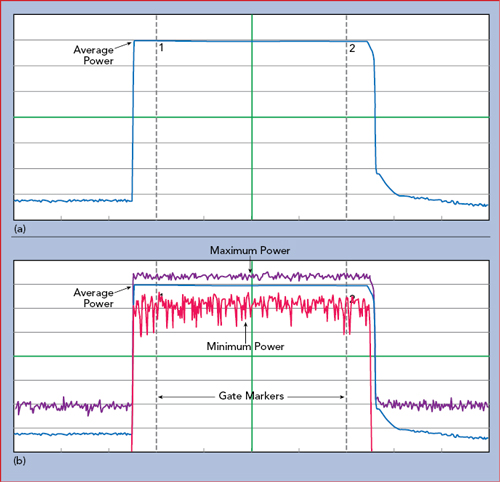
Figure 7 Unmodulated (a) and modulated (b) pulse power measurement.
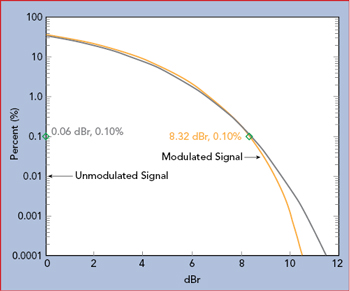
Figure 8 CCDF of unmodulated and OFDM-modulated pulses vs. theoretical Gaussian signal.
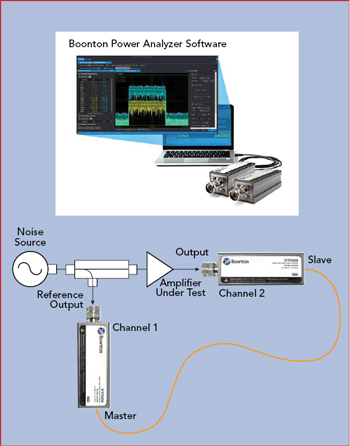
Figure 9 Amplifier measurement setup.
As one example of peak power meters, the Boonton power measurement portfolio includes two solutions with greater than 100 MHz video bandwidth: the 4500C with 125 MHz video bandwidth and the RTP5006 with 195 MHz, roughly 6× greater than most alternative products. Both models calculate and plot CCDF curves.
Figure 7 shows an 11 dBm, 10 μs pulse measured with the RTP5006 real-time peak power sensor. The RTP5006 provides three power values with each measurement: minimum, average and maximum. Figure 7a shows an unmodulated pulse where the minimum, average and maximum power are the same. Figure 7b shows a pulse modulated with a 2.5 GHz, 40 MHz bandwidth, −3 dBm signal generated with a Noisecom noise source, which approximates an OFDM signal. This shows the minimum, average and maximum power and the envelope of the modulated signal. The measurements can be gated to analyze the signal only when the pulse is on, disregarding transitions and off-time. The CCDF is calculated and plotted (see Figure 8). As expected, the non-modulated signal shows no appreciable peak power, while the modulated signal indicates a high PAPR and closely matches the CCDF of a theoretical Gaussian signal.
Some engineers may stop at the measurement of PAPR and calculation of CCDF at the output of an amplifier as representing amplifier performance. Knowing the output PAPR, they believe they can implement PAPR reduction techniques or apply IBO to optimize the amplifier performance. However, just looking at the output power of the amplifier may be misleading, as the output may already be in compression; measuring the input signal to the amplifier for reference is necessary.
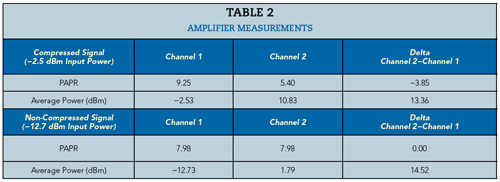
Figure 9 shows a test setup for measuring an amplifier’s input and output signals. The two sensor measurements are synchronized using a master/slave trigger. Figure 10 shows the input and output signals. Visually, there are no obvious issues; however, calculating the CCDFs shows the input and output PAPRs do not behave the same (see Figure 11). The output power is clearly compressed as seen in the lower PAPR measurements, resulting in a shift of the curve to the lower left relative to the input channel. By reducing the output power of the noise source and increasing the IBO, the PAPRs align (see Figure 12). This confirms that the amplifier was compressing the signal at the original input power level. Without measuring the input signal PAPR, this would not be apparent. A summary of the amplifier measurements in Table 2 shows with an input power level of −12.7 dBm, the output is not compressed. At an input level of −2.5 dBm, the compression is nearly 4 dB.
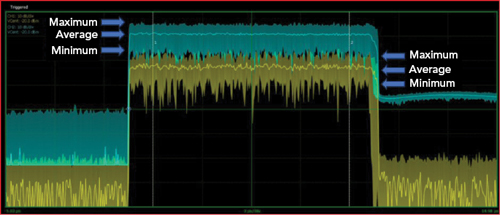
Figure 10 Measured amplifier input (yellow) and output (green) power.
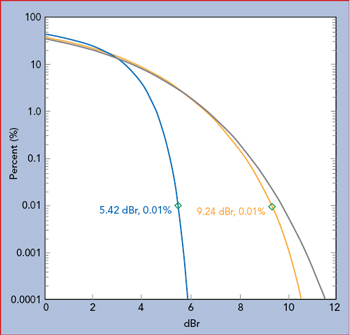
Figure 11 CCDF of amplifier input (yellow) vs. output (green) power shows significant compression, with a Gaussian signal shown for reference.
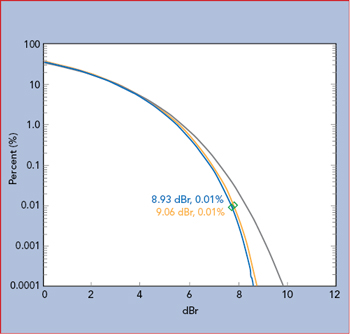
Figure 12 Reducing the noise source power reduces amplifier compression, confirmed by the improved alignment of the amplifier input (yellow) and output (green) CCDF curves.
OFDM-based systems often use QAM to modulate the subcarriers, and QAM is very sensitive to amplitude distortion. As the order of QAM increases to support higher data rates, that sensitivity increases. Relying only on average output power measurements, the observed compression would significantly understate the issue.
IMPORTANCE OF MODULATED SIGNAL MEASUREMENT
In some cases, engineers characterize amplifiers without modulation because signal sources with modulation-especially at the higher frequencies, such as the bands targeted for 5G-can be very expensive. However, with Gaussian noise removed and the input signal returned to its original value, compression is not observed. This highlights the importance of using modulated signals and peak RF power meters for characterizing amplifier performance, especially when evaluating PAPR reduction techniques. To avoid the cost of modulated signal sources, noise sources provide a much more cost-effective modulation source that closely models high subcarrier OFDM signals. Once the amplifier has been characterized with a Gaussian noise source, engineers can implement PAPR reduction techniques, comparing the results with an RF peak power meter.
SUMMARY
The increasing demand for information has led to increasingly complex data modulation to support high data rates and spectral efficiency. One of the most widely used technologies is OFDM; however, it has the disadvantage of having a high PAPR, which can challenge component performance. This leads many engineers to investigate techniques to reduce PAPR. RF peak power meters and noise sources are the instruments of choice for measuring the effectiveness of these techniques in a simple, cost-effective manner.
References
- “Orthogonal Frequency-Division Multiplexing,” Wikipedia, en.wikipedia.org/wiki/Orthogonal_frequency-division_multiplexing.
- Y. Rahmatallah and S. Mohan, “IEEE Peak-To-Average Power Ratio Reduction in OFDM Systems: A Survey And Taxonomy,” IEEE Communications Surveys & Tutorials, Vol. 15, No. 4, 2013, pp. 1567–1592.
- R. V. Nee and R. Prasad, “OFDM for Wireless Multimedia Communications,” Artech House, Norwood, Mass., March 2000.
