Doppler beam sharpening (DBS) is an effective technique to improve the azimuth resolution of airborne pulse Doppler radar in its air-to-ground mode. This article describes new developments of DBS in China. First, the basic theory of DBS imaging is presented. Then some key steps of the implementation of DBS are discussed in detail. Due to the fact that the airborne Inertial Navigation Units (INU) measurement errors are too large in Chinese radar systems, two new Doppler centroid estimation algorithms in frequency-domain and time-domain are proposed. In addition, the precision of estimation is improved significantly. The flowchart of signal processing is also presented. Finally, these algorithms are applied to some raw radar data. The imaging results prove their validity.
Modern fighters always take up multiple missions on the battlefield, such as scout, air-to-air interception and air-to-ground attack. Thus, it is required that airborne radar should have simultaneous air-to-air mode and air-to-ground mode capability. Considering the limitation of the carrying capacity in the head of the fighter, pulse Doppler (PD) radar is usually used. The PD radar can suppress the strong background clutter with the technique of Doppler spectrum separation. The high resolution in the range direction can be realized by pulse compression. However, it is more difficult to achieve high resolution in the azimuth direction. Generally the resolution of an antenna beam in the azimuth direction is proportional to the range between radar and target. Suppose the range between radar and target is 50 km, and the antenna's 3 dB beamwidth is 3.6°, the real beam resolution in the azimuth direction is 3.14 km. On condition that the range between radar and target does not change, the antenna beamwidth must be reduced to improve the azimuth resolution. However, the reduction of antenna beamwidth is very difficult due to other limitations. These limitations exist because the target is much smaller than the resolution cell and the energy of target is much smaller than the energy of ground clutter. Therefore, the target can hardly be detected.
To overcome the fault of real aperture resolution, some researchers proposed that the techniques of Doppler analysis could be used to improve the azimuth resolution. This approach is called the synthetic aperture radar (SAR) technique. Currently spotlight SAR can get high azimuth resolution under 1 m. However, precise motion compensation and complicated operations are required. To reduce the system complexity and the requirement of INU measurement precision, the DBS technique, which can construct unfocused radar images at a high squint angle and in a large scanning field, has been implemented in many airborne PD radar systems.
In 1951, C. Wiley proposed the principle of DBS, and the first unfocused radar image was produced in 1953. From that time the technique of DBS developed quickly. Currently, new PD radars, whose Doppler sharpening ratio can reach 128:1, have been put into practice. In China, DBS research has been in development for more than fifteen years, and has produced numerous papers.14,79 Yinging1 , for example, introduced the principle of DBS based on Doppler spectrum analysis, while Zhizhong2 discussed the selection of pulse repetition frequency (PRF) and the scanning mode in DBS imaging. In addition, some applied PD radar systems have been developed by Nanjing Research Institute of Electronic Technology (NRIET) and other institutes.3 This article presents recent research results on DBS imaging in cooperation with NRIET of China. First, the basic principle of DBS imaging is analyzed. Then some key steps in DBS processing are discussed. Due to the fact that the measurement errors of INU affect the precision of Doppler centroid estimation, some improved algorithms in time-domain and frequency-domain are presented. Finally, some new DBS imaging results of an experimental PD radar are presented.
PRINCIPLE OF DBS
DBS can be regarded as a certain mode of SAR. The angles between the targets located in different azimuth directions and the aircraft flight course are different from one another. Thus, the radial velocities of the targets locating in different azimuth directions are also different from one another. Therefore, different Doppler frequencies are induced. If a set of narrow band filters are placed in the frequency-domain, whose center frequency is aimed at the centroid of Doppler spectrum in azimuth direction, and whose bandwidth covers the Doppler frequencies induced by all targets, targets located in different azimuth directions can be distinguished. Therefore, high resolution is achieved in the azimuth direction.
Figure 1 is the geometry of the ground target and airborne radar. The aircraft A, whose flight height is H, moves along the Y-axis at a uniform speed v. The azimuth and elevation angles of the PD radar mainlobe are  and Φ, respectively. The intersection between the centerline of mainlobe and the ground is P. The slant range between radar and point P is R. The antenna 3 dB beamwidth is ß and its wavelength is *. The Doppler frequency induced by the target which is located on point P is
and Φ, respectively. The intersection between the centerline of mainlobe and the ground is P. The slant range between radar and point P is R. The antenna 3 dB beamwidth is ß and its wavelength is *. The Doppler frequency induced by the target which is located on point P is

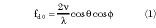
There are scatterers located in the same range gate R that have the same elevation angle Φ. However, their azimuth positions are different. That is to say, they have different Doppler shift. The Doppler bandwidth in the mainlobe irradiating area is
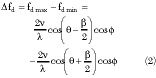
Considering that ß is very small, the Doppler bandwidth Δfd can be approximated to
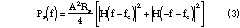
To sharpen the antenna's 3 dB mainlobe, the Doppler bandwidth Δfd should be divided. If the sharpening ratio is N, N narrowband filters should be used to divide Δfd , as shown in Figure 2.

In practice, N narrowband filters can be implemented by an N-point fast Fourier transform (FFT) operation. The radar PRF fr is set to correspond to the Doppler bandwidth Δfd and fd0 induced by the target located in the centerline of the mainlobe should be set to a position of fr /2. When N pulses are received by the PD radar at the frequency of fr , N-point FFT forms N narrowband filters in the frequency-domain. Therefore the targets locating in the mainlobe can be distinguished in azimuth.
DBS PROCESSING STEPS
PRF Selection
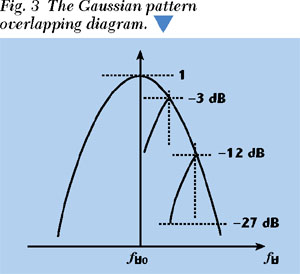
The azimuth Doppler bandwidth Δfd is the most important restriction on the radar PRF. To permit the set of narrowband filters to cover all Doppler frequencies of the ground targets, fr should be greater than or equal to Δfd . Suppose fr = mΔfd . If m = 1 is selected, the set of narrowband filters formed by the FFT can only cover the ground targets located in the radar 3 dB mainlobe irradiating area. The echoes coming from the scatters locating outside the 3 dB mainlobe irradiating area will overlap into the 3 dB mainlobe irradiating area. Thus, the sharpened image may be blurred. If m = 2 is selected, the antenna mainlobe is Gaussian, the overlapping boundary is 12 dB and the signal amplitude overlapping into the 3 dB mainlobe irradiating area is under 27 dB, as shown in Figure 3. This effect can be ignored. Considering that Δfd will change while the azimuth angle  changes, fr should also change with
changes, fr should also change with  continuously, that is, fr
continuously, that is, fr  sin
sin .
.
On the other hand, the antenna of an airborne PD radar will scan and may be at a large squint angle in the DBS mode. To get a radar image with a good visible impression, it is often required that the sharpening ratio remains invariable when  changes. The actual sharpening ratio s is
changes. The actual sharpening ratio s is
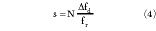
where N is the number of accumulated pulses (and also the number of FFT points). From Equation 4, it is clear that to keep s invariable, fr should be proportional to Δfd . That is to say, fr  sin
sin . This concept can be explained as follows: To keep the sharpening ratio invariable at different azimuth angles, the synthetic aperture range, which is perpendicular to the beam boresight, should also be invariable. Thus, the synthetic aperture time may be long when sin* is very small. Then fr should be reduced to keep the invariable pulse number, that is, to maintain the invariable sharpening ratio.
. This concept can be explained as follows: To keep the sharpening ratio invariable at different azimuth angles, the synthetic aperture range, which is perpendicular to the beam boresight, should also be invariable. Thus, the synthetic aperture time may be long when sin* is very small. Then fr should be reduced to keep the invariable pulse number, that is, to maintain the invariable sharpening ratio.
From Equation 4, it seems that the sharpening ratio can be increased infinitely by prolonging the observation time and increasing the FFT points. Of course, this is impossible. The improvement of the sharpening ratio is limited by a few factors. The echo of an airborne PD radar at a squint angle is a linear frequency modulation (LFM) signal. If the observation time and FFT points are too long, the Doppler frequencies induced by the scatterers may extend beyond the bandwidth of the narrowband filters. The azimuth spectrum may spread. At the same time, too long an observation time may cause a scatterer to migrate from one resolution cell to another. That condition is called range migration. The correct coherent accumulation cannot be achieved.
SCANNING MODE SELECTION
In DBS mode, the antenna of the PD radar usually scans from 15° to 60°. When *< 15°, the Doppler bandwidth Δfd is very narrow. The azimuth resolution will degrade under a certain observation time. At the same time, the effects of range migration are serious. Thus, Doppler beam sharpening is very difficult when  < 15°. On the other hand, * = 60° is the upper limit of scanning, which is determined by the mechanical performance of the PD radar antenna. How to choose the mode of scanning from 15° to 60° is an important problem that deserves research. From the previous discussion, note that the radar PRF fr should be continuously proportional to sin
< 15°. On the other hand, * = 60° is the upper limit of scanning, which is determined by the mechanical performance of the PD radar antenna. How to choose the mode of scanning from 15° to 60° is an important problem that deserves research. From the previous discussion, note that the radar PRF fr should be continuously proportional to sin . In practice only a stepped PRF can be used to approximate the continuous increasing PRF. If the scanning angle of the PD radar antenna increases/decreases n steps during the scanning in its mainlobe 3 dB bandwidth ß, the antenna scanning rate ω should satisfy ωT = ß/n, whereT = N/fr , N is the number of accumulated pulses at a certain azimuth angle. Therefore
. In practice only a stepped PRF can be used to approximate the continuous increasing PRF. If the scanning angle of the PD radar antenna increases/decreases n steps during the scanning in its mainlobe 3 dB bandwidth ß, the antenna scanning rate ω should satisfy ωT = ß/n, whereT = N/fr , N is the number of accumulated pulses at a certain azimuth angle. Therefore
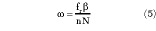
Zhizhong2 proposed two scanning modes that are often used in DBS. The first one is called sequential sharpened beams processing (SSBP). In this mode, fr and ω will step to the next values every other ß/N, where N is the sharpening ratio. This mode can keep the interval between every two sharpening angles invariable. However, its scanning rate ω is too low. If the sharpening ratio is N = 64, ω may change from 0.2°/s to 0.6°/s. It takes too long to complete an entire DBS map from * = 15° to 60°. The second scanning mode is called consolidated sharpened beams processing (CSBP). fr and ω will step to the next values every other ß/n, where n is a small integer which is determined by the number of subimages used in the non-coherent accumulation. In this mode, every set of N/n sharpening beams use the same fr and ω. Strictly speaking, it causes the beamwidth of every sharpening beam to make tiny changes. But its scanning rate is very high compared with SSBP. It may take less than 10s to scan from 15° to 60°. How does one choose which scanning mode will be used in practice? It depends on the requirements of the sharpening ratio and the complete processing time. When only a small sharpening ratio is required, such as N = 8, the difference between the two sharpening beamwidths is evident in CSBP, while SSBP will keep the same sharpening beamwidth and the duration of scanning will not be too long for the small sharpening ratio. So SSBP may be used in this case. If the required sharpening ratio is large, the difference between the two sharpening beamwidths can be ignored in CSBP. It will not affect the quality of images and the scanning rate can also be significantly increased. Thus, CSBP may be chosen in the case of a large sharpening ratio. Based on this analysis, CSBP is used in the DBS imaging of airborne PD radars developed by NRIET.
MOTION COMPENSATION
The motion compensation contains two parts. The first one is the compensation on maneuvering, that is, the compensation on the aberrancy from the uniform linear motion of the aircraft. The second one is the compensation on the uniform linear motion itself.
Ideally the aircraft maintains uniform linear motion in the DBS mode, and its posture also is constant. When the aircraft carries out a maneuvering motion, the DBS algorithm will be invalid. In addition, PD radars are usually installed in fighters. Even though the fighter does not engage in a maneuvering motion, it may deflect the ideal uniform linear motion due to disturbance of the atmosphere. The compensation for maneuvering can also be divided into two parts. The first one is posture compensation, which can compensate all posture changes of the aircraft, such as pitching, rolling and yawing, to correct the beam boresight to aim at the center of the imaging area. The second one is flight course compensation, to compensate for the variation of range between the radar and scatterers for the deflection of an ideal flight course. The above two compensations are based on the airborne INU system.4
On the other hand, when the antenna works at a squint angle, the relative speed between the radar and ground target is very high. The variety of range between radar and target could be 800 to 1200 m. Even though the radar aircraft maintains ideal uniform linear motion, range migration will also affect the imaging quality. Range migration compensation is also based on the airborne INU system. The reference function and phase to be compensated can be derived from the INU parameters. Then they are multiplied with the echo signals, and the classic DBS algorithm can be used to construct the radar image. It should be noted that measurement errors are inevitable in an INU system. These errors will degrade the precision of motion compensation and the quality of the image significantly. The effects of different errors on DBS imaging are very complicated and will be discussed in another article.
DOPPLER CENTROID ESTIMATION
After the motion compensation, the single-look radar image can be constructed with azimuth FFT on range compressed data. However, due to Doppler ambiguity, the center of the image is not the center of the beam boresighting area. These images can be used to construct the entire map in all scanning directions. The Doppler centroid must be estimated and the center of single-look images shifted. Then a correct ground map can be constructed. Thus, the estimation of the Doppler centroid fd0 is one of the most important steps in DBS imaging. Theoretically, if the parameters of aircraft motion and antenna boresighting are known, the current Doppler centroid fd0 can be computed precisely from Equation 1. In fact, these parameters are all presented by the airborne INU system. Usually the parameter errors are too large to be used in the estimation of the Doppler centroid. To solve this problem, many researchers proposed estimation techniques not based on INU parameters, but echo signals themselves.58 These techniques can be classified in the time-domain and frequency-domain.
In the frequency-domain, the azimuth spectrum is first obtained by azimuth FFT. Then its energy centroid can be regarded as the estimation of the Doppler centroid. Generally the amplitude of the azimuth spectrum is the same as the antenna pattern.5 First the azimuth spectrum can be calculated based on a preset Doppler centroid. To avoid the effects of random fluctuation, the azimuth spectrums in many range gates should be averaged. In the end the true Doppler centroid can be computed by using an iterative searching algorithm in the frequency-domain based on the energy centroid criterion.5 Guoqing7 also introduced some other techniques, such as the energy balance approach method and weighted range dimension fitting method, to improve the precision of the frequency-domain techniques. In conclusion, the frequency-domain techniques are all based on the energy centroid criterion, that is, the energy center of the azimuth spectrum is regarded as the estimation of the Doppler centroid. When the target scene is uniform, the energy center of azimuth spectrum is a good estimation of the Doppler centroid. But when the target scene is non-uniform, the energy center cannot replace the Doppler centroid. This inability is the inherent fault in frequency-domain techniques.
The amplitude of the azimuth spectrum should be the scattering intensity weighted by the antenna pattern in the azimuth direction. It can also be regarded as the antenna pattern weighted by the scattering intensity in the azimuth direction. To avoid the effects of a non-uniform scene on the energy distribution of the azimuth spectrum, the antenna pattern weighted by the scattering intensity in the azimuth direction should be used to match with the real azimuth spectrum. But how is the distribution of scattering intensity in the azimuth direction determined? Of course it is observed only from the current echo signal. Consider this problem in another way. If the same scene is observed from the direction which is perpendicular to the former, its energy distribution in the range direction is the former required energy distribution in the azimuth direction. Thus, if the target scene is observed from multi-directions, the required azimuth energy distribution in a certain direction can be calculated by the weighted average range profile in others directions. Then this average azimuth energy distribution can be used to weight on the antenna pattern. Reference function matching to the real azimuth spectrum is achieved. At last, match processing is achieved between the reference signal and azimuth spectrum. The position in which the maximum value is obtained is the true Doppler centroid. This kind of proposed weighted pattern match technique (WPMT) can entirely avoid the effects of a non-uniform scene on the precision of Doppler centroid estimation. In addition, the implementation of WPMT is not complicated. However, on real battlefields, it may be impossible to observe the same scene in many directions. At that time the WPMT cannot be used.
Time-domain techniques can estimate the Doppler centroid from the echo signals in the time-domain directly. Madsen6 and Guoqung, et al.8 introduce the principle of time-domain estimation based on the time-domain correlation function and the adaptive filter theory, respectively. They all use the average phase difference to calculate the Doppler centroid. If an echo signal in a certain range gate is s(t), the next one in the same range gate should be s(t Tr ) = s(t)exp(j2¼fd0 Tr ), where Tr = 1/fr is the pulse repetition interval (PRI). Then
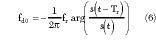
This equation is the principle of Doppler centroid estimation in the time-domain. The precision of time-domain techniques is very high because the echo fluctuation can be ignored. Of course it also cannot avoid the effects of a non-uniform scene entirely. Generally, the center frequency of an airborne PD radar is very high. The echo fluctuation is often evident. Thus, the Doppler centroid cannot be estimated from only two successive pulses. Madsen6 and Guoqung, et al.8 all propose that averaging multi-pulses should be used to reduce the effects of fluctuation. Based on the analysis and processing of so much experimental data, it was observed that even though many pulses are averaged, Doppler centroid estimation is still in a way random. To eliminate the effects of random phase errors, a curve fitting iterative technique (CFIT) is proposed. CFIT takes advantage of the correlation feature of Doppler centroids in different range gates and different azimuth directions. A curve fitting technique is used to eliminate the random errors. The basic steps of CFIT are as follows: (1) The data are pre-processed first by motion compensation and normalization. (2) Next the weak and abnormal signal is eliminated. Due to fluctuation and other reasons, the signal amplitudes in some range gates tend to zero. According to Equation 6, the estimation of the Doppler centroid is uncertain. Therefore, the weak signals and some abnormal signals should be eliminated before the Doppler centroid estimation. In the author's view, the threshold of elimination can be chosen as approximately 30 dB. (3) After the weak and abnormal signals are eliminated, the signals will be divided one by one to estimate the Doppler centroid from the first signal to the Mth one. Then many estimated values should be averaged using
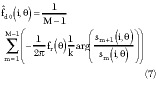
where
|
^ fd0 (i, |
= |
estimated value of the Doppler centroid in the ith range gate when the azimuth angle is |
|
sm (i, |
= |
mth echo signal |
|
sm+1 (i, |
= |
(m+1)th signal |
|
M |
= |
total number of signals after the weak and abnormal ones are eliminated |
|
k |
= |
difference of sequence numbers between the mth signal and the (m+1)th one |
It should be noted that the operation includes phase unwrapping, which can be calculated based on the INU parameters.
(4) To every azimuth angle  , the estimated values of the Doppler centroid in different range gates fd0 (i,
, the estimated values of the Doppler centroid in different range gates fd0 (i, ) are used to fit a curve. The scatterers located in different range gates have different elevation angles Φ. From Equation 1, it's easy to see that the Doppler frequency is proportional to the cosine of elevation angle. Generally the elevation angle is very small; the difference of * in the observation area is no more than several degrees. Thus, the curve fitting can be replaced by linear fitting. Finally, the fitted values based on the least mean square (LMS) errors criterion are adopted as the next estimated values of ^ f'd0 (i,
) are used to fit a curve. The scatterers located in different range gates have different elevation angles Φ. From Equation 1, it's easy to see that the Doppler frequency is proportional to the cosine of elevation angle. Generally the elevation angle is very small; the difference of * in the observation area is no more than several degrees. Thus, the curve fitting can be replaced by linear fitting. Finally, the fitted values based on the least mean square (LMS) errors criterion are adopted as the next estimated values of ^ f'd0 (i, ). (5) For every range gate, the estimated values of the Doppler centroid at different azimuth angles ^ f'd0 (i,
). (5) For every range gate, the estimated values of the Doppler centroid at different azimuth angles ^ f'd0 (i, ) are used to fit a curve. The Doppler centroids in different azimuth angles * are proportional to cos
) are used to fit a curve. The Doppler centroids in different azimuth angles * are proportional to cos . The curve to be fitted is determinate by the antenna scanning scope. Then the next estimated values ^ f"d0 (i,
. The curve to be fitted is determinate by the antenna scanning scope. Then the next estimated values ^ f"d0 (i, ) can be determined from the former ^ f'd0 (i,
) can be determined from the former ^ f'd0 (i, ). (6) The final step is to let ^ fd0 (i,
). (6) The final step is to let ^ fd0 (i, ) = ^ f"d0 (i,
) = ^ f"d0 (i, ) and go to the fourth step. Only if *^ f'd0 (i,
) and go to the fourth step. Only if *^ f'd0 (i, ) ^ f"d0 (i,*)* < *, where * is the supposed precision, will the iterative algorithm end. The last ^ fd0 (i,
) ^ f"d0 (i,*)* < *, where * is the supposed precision, will the iterative algorithm end. The last ^ fd0 (i, ) are determined.
) are determined.
In summary, two improved techniques of Doppler centroid estimation in time-domain and frequency-domain, WPMT and CFIT, have been proposed, respectively. In fact, the iterative algorithm in CFIT can also be used in frequency-domain techniques. However, the effects of a non-uniform scene are too serious in the energy centroid criterion. If the azimuth spectrums in many range gates are averaged to eliminate the effects of a non-uniform scene, the change of Doppler centroid in the range direction will be lost. Therefore this method has not been adopted. The WPMT and CFIT techniques will be discussed in detail in other articles.
SPECKLE REDUCTION OF SUBAPERTURE IMAGES
There are many scatterers in one resolution cell. The echo from this resolution cell is composed of the echo vectors from these scatterers. The ranges between these scatterers and the radar are different at different times. Their phases are uncorrelated with one another. As a result, their composed vector may be strengthened for in-phase, or may be weakened for off-phase combinations. Therefore, many speckles will appear in the radar image. However, these speckles do not represent real scatterers.
Because the speckles distribute randomly, they can be restrained by the non-coherent accumulation of multiple subaperture images. Generally the superposition of three to four frames of images can eliminate the effect of speckles. However, this simple technique reduces the azimuth resolution. Except for the method of non-coherent accumulation, many image-processing techniques can be used to eliminate the speckles in a DBS image. In these techniques, adaptive filtering in the local domain is effective, in which a slipping window is selected in the image, and the filtered value of the center pixel is calculated based on the other values of pixels in this window. Chunsheng, et al.9 analyzes these algorithms. It should be noted that the computational cost of these image-processing techniques is too large to be used in real time. Thus, the non-coherent accumulation of multiple subaperture images is often used in practice.
GEOMETRY CORRECTION AND PATCHING
After Doppler centroid estimation and speckle reduction, the subaperture image is constructed. However, this image is described in radar measurement coordinates, that is spherical coordinates (R,  , Φ). It should be transformed to the Cartesian coordinates (x, y, z). The transforming formulas are
, Φ). It should be transformed to the Cartesian coordinates (x, y, z). The transforming formulas are
x = Rcos sinΦ (8)
sinΦ (8)
y = Rcos cosΦ (9)
cosΦ (9)
z = Rsin* (10)
After the coordinate transform linear interpolation is often used based on the energy distribution criterion to correct the geometric distortion of the pixel distribution.
After the coordinate transform and the geometric distortion correction, the final subaperture images are obtained. They can be used to patch up the entire map. Generally the scope of one subaperture image is wider than the scanning step length. Suppose fr = 2Δfd , and the antenna 3 dB beamwidth is 3.6°, then the scope of one subaperture image is 7.2°. However, the step length of scanning may be 2°or 3°. Therefore, the successive subaperture images partially overlap each other. Some researchers take the view that the signal-to-noise ratio (SNR) in the edge of subaperture image is low (affected by the antenna pattern), and some signals out of the mainbeam also overlap into the edge of subaperture image. Therefore, this part of the subaperture image should be cut off. Only the center part of subaperture image should be used for the map patching. This method is called cut-off patching. In the processing of so much raw DBS data, it was found that the final images using the cut-off patching method have distinct patching traces, and smoothing techniques are required to eliminate them. The non-ideal normalization of data may cause this phenomenon. Another method was also tried, in which the overlapped subimages are used to patch. This is called overlap patching. The quality of images has no difference from the former method, but there are almost no patching traces. In addition, the anti-weighting of the antenna pattern is not required in the subaperture images when using the overlap patching method. The smooth images can be obtained by the superposition of overlapped parts of images. Thus, the latter method is thought to be better than the former one.
THE DBS PROCESSING FLOWCHART
In summary, the flowchart of DBS processing is shown in Figure 4. The motion compensation includes the compensation of the non-ideal uniform linear motion and compensation of the range variation between the target scene and radar in uniform linear motion. If the target scene is uniform, common frequency-domain techniques can be used to estimate the Doppler centroid. In the non-uniform case, WPMT can be used if observation in multi-directions is possible. Otherwise, CFIT may be used to improve the precision of Doppler centroid estimation. The method of speckle reduction may be chosen between the non-coherent accumulation method and the adaptive filtering method according to the processing time requirement. The last display processing can also choose different quantitative methods according to the different system requirements, such as linear quantification or logarithm quantification.

PROCESSING RESULTS OF RAW DBS DATA
Experimental PD Radar Parameters
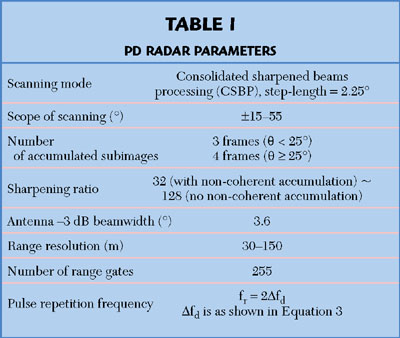
Nanjing Research Institute of Electronic Technology, in cooperation with Nanjing University of Science and Technology, made an experimental PD radar and obtained much raw DBS data. The parameters of PD radar are listed in Table 1.
Experimental Results Analysis
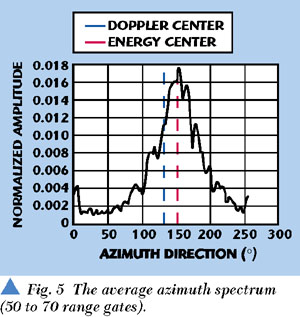
As stated previously, the Doppler centroid estimation technique in frequency-domain based on the energy centroid criterion has good performance to uniform scenes. Otherwise it will not work well. Figures 5 and 6 show the averaged azimuth spectrums of a semi-uniform scene in different range gates. It is clear that the Doppler centroid changes with the variation of the ground scene in different range gates. Even though the azimuth spectrums in all range gates are averaged, as shown in Figure 7, the correct Doppler centroid still cannot be determined. At the same time Doppler centroid changes in different range gates also can not be estimated. Due to the limitation of the experimental procedure, the WPMT technique cannot be confirmed, but its rationality is obvious.
|
|
|
|
|
|
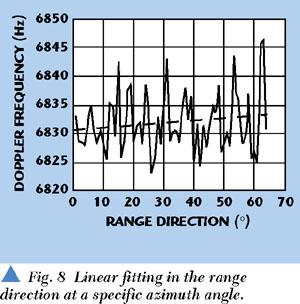
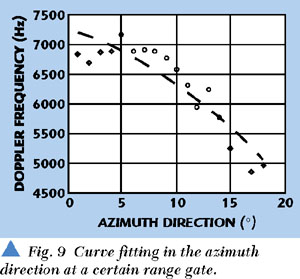
Relatively, the time-domain technique is more difficult to affect by the non-uniform scene compared with the frequency-domain technique in the estimation of the Doppler centroid. Using the CFIT, the precision of the Doppler centroid estimation can be improved significantly. Figure 8 shows the linear fitting result of the Doppler centroid in different range gates and at a certain azimuth angle. Figure 9 shows the next curve fitting result at different azimuth angles. Usually after three iterations the results may be convergent. Figure 10 shows the final estimation of the Doppler centroid in different range gates and at different azimuth angles.
|
|
|
|
|
|
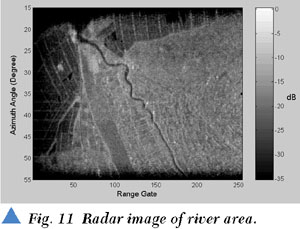
Due to the length of this article, the comparison of different speckle reduction and patching techniques will not be displayed here. Some of the final DBS imaging results are shown in Figures 11, 12, 13 and 14. In these images CFIT is used to estimate the Doppler centroid and the non-coherent accumulation method is used to reduce the speckles in radar images. The subaperture images are patched up by the overlap patching technique. No further smoothing techniques are applied to these images. From the last DBS images, the river, lake, hill and coast can easily be distinguished from the others. The imaging results testify to the effectiveness of the techniques proposed in this article.
|
|
|
|
|
|
CONCLUSION
DBS has been shown to be an effective technique to improve the azimuth resolution in airborne PD radars. In China, the research on DBS has been well developed. In addition to many papers, some applied airborne DBS radar systems have been put to use. This article introduces the recent development of DBS in China. According to the performance of Chinese radar systems, some improved methods are presented on Doppler centroid estimation. Many imaging results based on raw radar data prove the validity of these methods. In short, the DBS technique has been well developed in theory and implementation and will play a key role on the modern battlefield.
ACKNOWLEDGMENT
This article was supported by the Department of Airborne Electronic Technology in NRIET. Professor Huide Cai provided the authors help in the experiments and raw data processing. Professor Jinlin Ni, Chief Engineer in NRIET, also proposed reasonable advice to the research work. The authors thank them. *
References
1. Zhou Yinqing, "Doppler Beam Sharping Technique for Airborne Pulse Doppler Radar," Acta Aeronautica Et Astronautica Sinica, Vol. 9, No. 12, December 1988, pp. 574581.
2. Zhang Zhizhong, "The Discussion on Some Problems of DBS Theory and Implementation," Modern Radar, Vol. 13, No. 2, April 1991, pp. 112.
3. Mao Shiyi, Li Shaohong, Huang Yonghong and Chen Yuanzhi, "Study of Real-time Image by DBS on Airborne PD Radar," Acta Electronica Sinica, Vol. 28, No. 3, March 2000, pp. 3234.
4. Zhang Qingwen and Zhang Jianyun, "The Study of Motion Compensation for Doppler Beam Sharping," Acta Aeronautica Et Astronautica Sinica, Vol. 15, No. 11, November 1994, pp. 13481356.
5. F.K. Li, D.N. Held, J. Curlander and C. Wu, "Doppler Parameter Estimation of Synthetic Aperture Radar," IEEE Transactions on Geoscience and Remote Sensing, Vol. GE-23, No. 1, January 1985, pp. 4756.
6. S.N. Madsen, "Estimating the Doppler Centroid of SAR Data," IEEE Transactions on Aerospace and Electronic Systems, Vol. AES-25, No. 2, March 1989, pp. 134140.
7. Liu Guoqing and Huang Shunji, "Improved Doppler Centroid Estimation for Spaceborne SAR Data," Signal Processing, Vol. 10, No. 3, September 1994, pp. 156160.
8. Zhao Zhiqing, Liu Xingfan and Gu Deren, "Doppler Parameters Estimation for SAR in Time-domain," Signal Processing, Vol. 11, No. 1, March 1995, pp. 2630.
9. Li Chunsheng, Yang Ying, Chen Jie, Huang Yan and Zhou Yinqing, "Speckle Reduction for High Resolution One-look Spaceborne SAR Images, Acta Electronica Sinica, Vol. 28, No. 3, March 2000, pp. 1316.
|
|







 Hongbo Sun received his BSc and MS degrees, both in electronics engineering, from Nanjing University of Science and Technology (NUST), P.R. China, in 1997 and 1999, respectively. He is currently a PhD candidate in the Research Center of Electronics Engineering Technology, NUST. His research interests include synthetic aperture radar imaging, ground clutter cancellation, moving target detection and nonstationary signal processing.
Hongbo Sun received his BSc and MS degrees, both in electronics engineering, from Nanjing University of Science and Technology (NUST), P.R. China, in 1997 and 1999, respectively. He is currently a PhD candidate in the Research Center of Electronics Engineering Technology, NUST. His research interests include synthetic aperture radar imaging, ground clutter cancellation, moving target detection and nonstationary signal processing. Guosui Liu graduated from the department of radar engineering, Military Institute of Engineering, P.R. China, in 1953. For the past 50 years, he has performed teaching and researching in radar system and signal processing. Currently he is a professor in the department of electronics at Nanjing University of Science and Technology, P.R. China. He is also a fellow of CIE, a member of the Academy for Chinese Ordnance and a senior member of IEEE.
Guosui Liu graduated from the department of radar engineering, Military Institute of Engineering, P.R. China, in 1953. For the past 50 years, he has performed teaching and researching in radar system and signal processing. Currently he is a professor in the department of electronics at Nanjing University of Science and Technology, P.R. China. He is also a fellow of CIE, a member of the Academy for Chinese Ordnance and a senior member of IEEE. Hong Gu received his BSc degree from Ease China Institute of Technology in 1988, his MS degree from Nanjing University of Science and Technology in 1991, and his PhD degree from Xidian University in 1995, all in electronics engineering. His research interests are random signal radar system, radar signal processing and high speed digital signal processing.
Hong Gu received his BSc degree from Ease China Institute of Technology in 1988, his MS degree from Nanjing University of Science and Technology in 1991, and his PhD degree from Xidian University in 1995, all in electronics engineering. His research interests are random signal radar system, radar signal processing and high speed digital signal processing. Weimin Su received his BSc in physics at Xuzhou Normal University in 1986, his MS and PhD degrees, both in electronics engineering, from Nanjing University of Science and Technology in 1992 and 1997, respectively. His research interests include array signal processing and radar signal processing.
Weimin Su received his BSc in physics at Xuzhou Normal University in 1986, his MS and PhD degrees, both in electronics engineering, from Nanjing University of Science and Technology in 1992 and 1997, respectively. His research interests include array signal processing and radar signal processing.