A High Order Frequency Multiplier for Low Power Applications
D.R. Lang
Comtech/EFData
Tempe, AZ
Direct frequency multipliers are commonly used in applications where the added phase noise or circuit complexity of a phase-locked loop is undesirable. At power levels above 1 mW, varactors or step recovery diodes can supply the needed power directly, but generally require RF drive power levels that are incompatible with the low currents and voltages in modern portable products. An injection-locked oscillator (ILO) can supply the desired harmonic efficiently, but it will continue to deliver output power at the wrong frequency if the tuning is incorrect due to aging, or if the input level becomes insufficient to lock the oscillator at the desired multiple. There is no comparable threshold problem if an overdriven amplifier is used as a harmonic generator; however, both the output power and DC-to-RF efficiency are likely to become impractically small for large values of multiplication N.
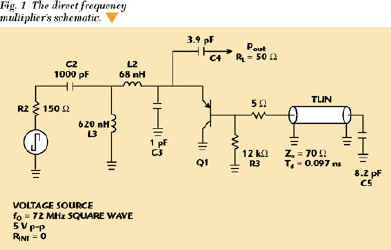
The circuit shown in Figure 1, along with its conceptual model, avoids these problems. Since no DC bias is provided for Q1 , there is no measurable RF output power when the fundamental frequency input signal is removed. The output is a damped sinusoid; hence, the output power can be concentrated in a few spectral lines clustered around the desired harmonic, rather than in the wideband comb spectrum characteristic of an impulse generator or overdriven amplifier.
BACKGROUND
It is assumed that the input to a broadband (impulse) frequency multiplier is a CW input signal Ao cos(2p FR t + f o ) and that the output is observed only after the DC bias terms at all internal nodes have reached their steady-state values. When the multiplier output is sampled at a rate FSAMP > 2FR , its output frequency components will be aliased down to the frequency band from DC to FR . The sampler output will be limited to FR provided the multiplier output consists of only integral multiples of the input frequency and is free of spurious (nonharmonically related) components. Stated another way, the phase offset values f n in the multiplier output spectrum An cos(N2p FR t + f n ) must be stationary between successive cycles of the input reference signal.
An ILO consists of a (generally) narrowband oscillator, which has an intrinsic or unlocked frequency FUL close to the desired, locked output frequency FO . The ILO is provided with an additional input port for insertion of a reference signal FR = FO /M. When M = 1, the structure is termed an injection-locked amplifier (ILA). When an ILO is used as a multiplier, the reference frequency is injected into the oscillator feedback loop with sufficient amplitude to reset the f n terms between input cycles, and the ILO output effectively consists only of FO = MFR . Numerous papers describe the design and adjustment of ILOs.1
The multiplier input signal at FR is nominally a square wave from a CMOS or equivalent logic buffer used as a low impedance voltage source. Since the duty cycle of most system reference clocks is close to 50 percent, this value is used in the analysis. The DC component of the clock signal is blocked, and R3 allows forward bias of Q1 only during the negative-going half of the reference cycle. No general significance is claimed for the choice of the collector for the grounded terminal of Q1 . At the operating frequency used in the original design, this configuration required a smaller load admittance transformation ratio than alternate topologies evaluated.
The initial design procedure parallels that of any one-port oscillator. The circuit elements are adjusted to meet the minimum requirements for oscillation at FO as
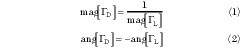
where G D and G L represent the reflection coefficients of the oscillator and load, respectively.
Next, the effects of the active and passive component variations within the oscillator and load are examined to verify that no reasonable combination of G D and G L near FO violates the Kurokawa criteria for steady-state oscillator stability.4,5 These criteria are sufficient but not necessary for steady-state stability at a specific frequency and power level. When G D can be accurately represented as impedance RD ± jXD (series resonant oscillator), the first criterion is
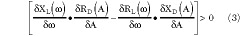
Two empirically based simplifying assumptions generally apply:
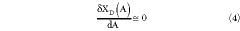

When G D can be represented as an admittance GD ± jBD , the shunt resonant counterpart of Equation 3 applies such that
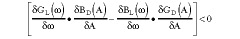
The dual versions of the simplifying assumptions in Equations 4 and 5 are
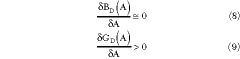
and the admittance form of the result of Equation 7 is
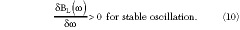
The criterion of Equation 3 is, for example, sufficient to ensure that when an initial operating point [PO (ZL ), FO (ZL )] migrates to a new point [PO (ZL2 ), FO (ZL2 )] due to a change in load impedance ZL2 = ZL + d Z, the oscillator will return to [PO (ZL ), FO (ZL )] when d Z = 0. (For example, the oscillator tuning will not exhibit hysteresis or moding.)
The idealized categorization of an oscillator as essentially series or shunt resonant may affect the choice of load topology. Consider a series resonant oscillator terminated with a shunt resonant load, where
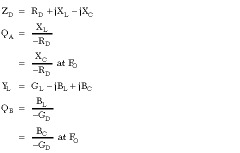
Now YU is defined as the admittance of the previously described network, measured at the shunt end, with only GL removed. It is easy to verify that for arbitrarily closely spaced frequencies F1 and F2 , QA and QB (QA > QB ) can be determined such that YUF1 = YUF2 ; that is, oscillation is possible on both frequencies. When QA < QB , the slope of d BU (w )/d (w )is dominated by the shunt elements and no frequency ambiguity exists. If the above exercise is repeated with a shunt resonant oscillator terminated with a series resonant load, where ZU is the impedance looking into the load end with RL removed and QA and QB are as previously defined, then frequency ambiguity exists for QB > QA , and conversely. An example of a series topology oscillator incorrectly terminated with a shunt resonant load (and its resulting undesirable tuning behavior) is provided by Hamilton.6
DESIGN DETAIL
The following design procedure is for a multiplier currently used in volume production for equipment qualified over the -40° to +65°C environment. For this design, FR = 72 MHz, N = 20 and PO >= -15 dBm at FO = 1440 MHz, and the nominal current demand is 6 mA at +5 V. In the end application, an inexpensive surface acoustic wave (SAW) bandpass filter was used to suppress the N = 19 and N = 21 harmonics. The SAW filter port impedance ZL is poorly defined outside of a narrow bandwidth centered on the desired N = 20 harmonic.
Since the Spice parameters of the MMBR901 bipolar junction transistor (BJT) were not readily available, a modified hybrid-pi bipolar model,3 shown in Figure 2, was created. In this model, both D1 and D2 are ideal Si diodes with negligible junction capacitance. With both the base resistance and the dynamic resistance of D1 replaced by RA , element optimization is used to force the model's small-signal S parameters to match the published device S parameters to an accuracy sufficient for the time domain simulation. Figure 3 shows the BJT's linear model. The model's small-signal S parameters are listed in Table 1.



With C4 omitted, G D is quite accurately represented by a shunt topology. A one-port Touchstone linear analysis of the multiplier circuit verified that Re[YD ] > 0 from 100 MHz to 10 GHz (excluding the operating band) and Re[YD ] + Re[YL ] < 0 within the operating band (1440 ± 100 MHz) after optimization of TLIN, C5 , C4 and C3 . As with any active circuit, failure to verify that potentially unstable regions are confined to the desired frequency band creates a risk of spurious signal generation. Although the decision to insert C4 at this port appears to be a violation of the criterion in Equation 10, the specific broadband input impedance of the SAW filter transformed through C4 was sufficiently close to the required shunt topology that stability was ensured.
Next, the multiplier is modeled using a time domain simulator (such as PSpice) to verify output level, biasing and drive margin. The negative-going transition of VS at the start of the on period defines the initial amplitude and phase offset terms An and f n for the sinusoidal burst. During the off period, Q1 is inactive and undesired contributions to the stationary values of f n are minimized to the extent that the harmonic amplitudes An decay to negligible levels between reference cycles. The net series impedance of C2 , R2 and L2 is made large enough that the effect on ZD is negligible, C2 and R2 are adjusted so that the average current through Q1 does not exceed the desired supply limit and the combination of C2 and L2 determines the RF pulse width. Small changes (20 percent or less) in the duty cycle have very little effect on output power. For the fractional pulse width ratio Tpw used (0.27), the multiplier output spectrum is wide enough that no tuning or selection of TLIN or C5 is required. Some suggested limiting values of remaining components are listed in Table 2.
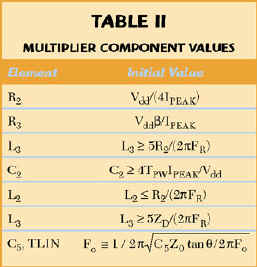
Figure 4 shows the output of a PSpice simulation for the 1440 MHz multiplier using the nonlinear BJT model. For practical cases, modeling the output burst envelope as a damped exponential function is consistent with both time domain simulations and physical measurements. Equations 11 to 21 and Figure 5 define the parameters used in the Fourier representations of both the baseband and RF burst exponential function. If the available time domain simulator has discrete Fourier transform capability, the spectral output amplitudes can be evaluated directly. If not, the amplitude and width of the RF output pulse envelope can be visually estimated and Equations 11 to 21 applied to obtain the harmonic amplitudes.



The scaling constant 2.4464 in the fractional pulse width expression is the difference between the two t parameter values for which the pulse amplitude is half the maximum value such that

where Vpeak = 0.5 (the measured or simulated peak-to-peak RF output magnitude) and Vmax is defined by Equation 13.
Note that Equations 11 to 21 are listed in a format that is directly insertable into a spreadsheet such as Excel. An example of the burst waveform is shown in Figure 6.

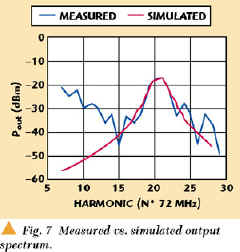
Both the calculated spectrum of the time domain simulation and the measured spectrum are plotted in Figure 7. The measured spectrum includes both the active multiplier contribution and the harmonics due to the square wave reference waveform coupled directly through C2 , C4 , L2 and R2 .
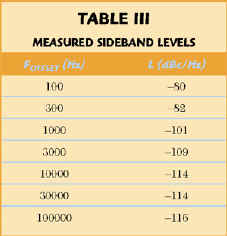
The phase noise of the above multiplier was evaluated by comparing its performance with that of a 1440 MHz brute force multiplier utilizing limiting diodes and gain stages. Both multipliers were driven by the same 72 MHz phase-locked crystal oscillator reference source; no significant difference between the output phase noise spectra of the two multipliers was observed. The sideband levels measured for both multipliers are listed in Table 3.
CONCLUSION
A direct frequency multiplier has been described that is suitable for high order, low power multiplier applications. A modified model using PSpice was used to optimize the required circuit component values and analyze the multiplier's performance. The resulting multiplier's phase noise performance compared favorably with a brute force multiplier at 1440 MHz. *
References
1. Vasil Uzunoglu, "Oscillator Network Performs a Diverse Range of Functions," Microwaves & RF, August 1996, pp. 115128.
2. Edmar Camargo, Design of FET Multipliers and Harmonic Oscillators, Artech House, 1998.
3. Jose E. Schutt-Aine, "Determination of a Small-signal Model for Ion-implanted Microwave Transistors," IEEE Transactions on Electron Devices, Vol. ED-30, No. 7, July 1983, pp. 750758.
4. K. Kurokawa, "Some Basic Characteristics of Broadband Negative Resistance Oscillator Circuits," Bell System Technical Journal, JulyAugust 1969, pp. 19371955.
5. Robert Soares (editor), GaAs MESFET Circuit Design, Artech House, 1988, pp. 350355.
6. Steve Hamilton, "Microwave Oscillator Circuits," Microwave Journal, Vol. 21, No. 4, April 1978, pp. 6384.
7. Advanced Bipolar Transistor Modeling Techniques, Hewlett-Packard Application Note 1201-4, July 1991.
8. Harmonic Generation Using Step Recovery Diodes and SRD Modules, Hewlett-Packard Application Note 920.
David R. Lang is a principal member of the technical staff at Comtech/EFData. Prior to joining Comtech, Lang served with Adaptive Broadband and Motorola, specializing in RF/microwave circuit design for both military and cellular products. His most recent work includes the detailed development and design of commercial, C- and Ku-band satellite terminal systems.
