LOW NOISE VCOS: KEY COMPONENTS FOR BASE STATIONS

TUTORIAL

LOW NOISE VCOS: KEY COMPONENTS FOR BASE STATIONS

FRANK BABERG

Tekelec Temex

Munich, Germany

 

The great economic success of modern mobile radio systems such as GSM and the digital communication system (DCS) means even greater utilization of the capacity of existing channels. Therefore, it is immensely important to adhere to GSM specifications exactly. In GSM, the available frequency range is divided according to the frequency division multiple access (FDMA) procedure1,2 into radio channels of 200 kHz bandwidth each. On the other hand, each radio channel is divided into eight traffic channels through a time multiplexing (TDMA) procedure1,2 and contains information (voice and signals) in so-called bursts. In the case of a channel width of 200 kHz, this allocation typically produces 124 GSM channels with a bandwidth of 25 MHz (the first channel is not normally used) and 372 DCS channels with a bandwidth of 75 MHz.

Fig. 1 Block diagram of a base station.

The block diagram shown in Figure 1 displays the frequency processing that takes place in a base station. In the transmitter (TX), the working signal must be converted into an RF signal; in the reception path (RX), the received RF signal is converted into one (or two) fixed intermediate frequencies (IF). Each of the two conversion processes requires an LO. Since a base station works in full duplex mode, the RX and TX paths must be viewed separately and have their own LOs. With mobile phones, a common LO is sufficient because it features a half-duplex operation due to the TDMA time slots.

Fig. 2 Switching operation of a Clapp oscillator.

Fig. 3 The Clapp oscillator's RF equivalent circuit.

Fig. 4 The Clapp oscillator's simplified equivalent circuit.

Obviously, the actual concepts used can differ significantly from this configuration. For example, the RX path also can be constructed using only one IF. In modern communication systems, a synthesizer is normally used; that is, an oscillator is synchronized through a reference fed to a phase-locked loop (PLL). There are a number of different ways to create the reference, such as deriving it from the fixed network clock or by synchronization via the Global Positioning System. However, these methods are not discussed in this article. A VCO is used as an LO because its frequency is dependent on an applied direct voltage. Thus, the VCO can be switched to the various channel frequencies relatively simply and quickly.

 

VCO STRUCTURES

Microwave oscillators are typically analyzed using the concept of negative resistance.3 When designing oscillators, various basic switching operations can be found in the literature, such as the Hartley-Meissner or Colpitts switching operations. The so-called Clapp switching operation has proven itself in VCOs in particular. The Clapp switching operation is very similar to the Colpitts switching operation, only the inductance is replaced by a resonant circuit, as shown in Figure 2. The equivalent circuit for the Clapp oscillator is shown in Figure 3, restricted to the RF components that are important for the operation. Figure 4 shows the simplified equivalent circuit diagram, displaying only the basic principle. The impedance of the serial resonant circuit can be expressed as

Thus, from Equation 1, the oscillation condition to produce a negative resistance becomes

The resulting frequency from the series connection of the three capacitors is found to be

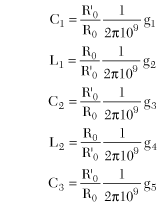
In RF technology, the oscillator is often shown as a four-pole amplifier with amplification V, whose output voltage is fed back to the input via a feedback network. If the Clapp oscillator is drawn as shown in Figure 5 (introducing a virtual ground), then the four-pole switching operation becomes evident.

In order to now determine the frequency of the oscillator using a direct voltage, one of the capacitors is replaced by a junction varactor. This component exploits the junction capacity of a diode operated in the reverse direction and is dependent on the reverse voltage applied. Analogous to a capacitor, the junction capacity of a PN junction is dependent on the cross-section surface and width of the junction. A theoretical analysis determines the relationship for the voltage dependency of the junction capacity2 as

In this relationship, C1 is the junction capacity Cj where V = VR, Cj0 at VR = 0 V, VD = the diffusion potential (approximately 0.65 V for silicon) and VR = the reverse voltage applied. The exponent m depends on the course of doping and is decisive for the voltage dependency of the junction capacity. In a diffused junction, the transition of the acceptor density NA (P area) is linear with respect to the donor density ND (N area). In this case, m = 0.33. With an abrupt junction, the transfer is carried out suddenly. In this case, m = 0.5. If a particularly strong dependency of the junction capacity on the voltage is required, m must be > 0.5. In this case, the doping density must be greater than for the abrupt junction. Such doping profiles are called hyperabrupt.

Fig. 5 Feedback in the Clapp oscillator; (a) the physical equivalent circuit, (b) introduction of virtual ground and (c) a four-pole representation.

Fig. 6 Equivalent circuit of the junction varactor in its case.

Fig. 7 A ceramic coaxial resonator's (a) structure and (b) equivalent circuit.

Figure 6 shows the small-signal equivalent circuit diagram of a junction varactor. The resistance Rs takes into consideration the reverse current of the diode and should be as large as possible in the interest of low noise (shot noise). In the case of higher frequencies, the bulk resistances become most noticeable. The influence of the case is described by the series inductance LG as well as the case capacity CG.

In addition to the capacity relationship C1/Cj0, the quality factor Q is a decisive characteristic. Analogous to the capacitor, the Q of the varactor is also defined as the relationship between the reactive and the active performance. From the simplified equivalent circuit, CT = Cj + CG, thus resulting in

Basically, the quality of abrupt junction crossings is significantly better than that of hyperabrupt crossings. However, very high reverse voltages of up to 90 V are required to achieve sufficiently large capacity variations. These high reverse voltages are required because, in the case of voltages (which lie significantly below the breakdown voltage), the reverse zone is only partially purged. The ohmic resistance still lies within the non-purged zone in series with the capacitance. For these reasons, hyperabrupt junctions mainly are used as oscillating circuit capacitors. In selecting a suitable varactor, it is also important that the connection between the reverse voltage and junction capacity be defined over as wide a range as possible.

 

PHASE NOISE PROPERTIES

Since modern high Q capacitors offer excellent quality,4,5 the selection of inductance L (in addition to the varactor) determines the phase noise to a significant extent. In the case of low phase noise requirements, the inductance can be realized through a coil printed onto the PCB. Better results are obtained by using air-core reactors in a surface-mount device.

The best characteristics are obtained using coaxial resonators, as shown in Figure 7. Ceramic resonators are shaped as cubes with a coaxial bore. The inner and outer surfaces are metallized. The capacity, inductance and resistance of the metallization provide an RF resonant circuit that oscillates in the TEM mode. The quarter-wave l/4 types are particularly space-saving. The additional metallization of an end face creates the required short circuit.

The resonance frequency is obtained from the relative permittivity and the length of the resonator. Basically, the length l for l/4 resonators is determined using

Dielectric values between er = 20 and 78 are available. The Q is almost exclusively determined by the final conductivity of the metallization to a value of Q < 800. Where higher Qs are required, a special silver metallization is recommended; in the case of price-sensitive applications, a copper-plated metallization is preferred. The no-load operating Q (Q0) is defined as the quotient of the resonant frequency and 3 dB bandwidth B3dB of the resonance response curve:

Q0 increases in the first approximation by Œ'f. Higher Q values can be achieved using larger cross-section measurements where it is then critical to integrate the resonator into the normally small VCO case.

 

VCO CHARACTERISTICS

VCOs are customer-specific modules. Each user design is different and, thus, the VCO modules must be adapted to customer specifications. Typical VCO performance specifications are listed in Table 1.6 These details can only be used as guide values for typical designs.

Phase noise is the most critical parameter for designing a VCO and, therefore, must be specified with particular care. In the case of sensitive pre-amplifiers, normally only the amplitude noise is taken into consideration as it characterizes the sensitivity of the amplifier. On the other hand, with oscillators, the amplitude noise plays only a subordinate role. What is decisive here are the stochastic changes in the zero transits of the sinusoidal oscillation created by the oscillator. Thus, the phase noise characteristic describes the relationship of the carrier level to the noise level in the environment of the carrier frequency. This relationship is described as a function x = F(fm), depending on the carrier offset. The fundamental significance of the phase noise is that it determines the interference in the neighboring channel. Therefore, a typical VCO specification states values of phase noise depending on the carrier offset.

The phase noise of a VCO has been observed in numerous theoretical experiments,6,7 and is described using

where

x(fm) = ratio of the phase noise in a 1 Hz bandwidth to the common VCO output level (dBc/Hz)

fm = carrier frequency offset

f0 = carrier frequency

fc = noise edge of the flicker or 1/f noise of the active oscillator

Qload = Q of the loaded resonator (resonance circuit with active load and parasitic elements)

F = noise figure of the four-pole active oscillator

K = Boltzmann constant (k = 1.38 ¥ 10&ndash;23 J/K)

T = temperature in Kelvins

Pav = oscillator output power level

R = equivalent noise resistance of the varactor

V0 = voltage amplification of the oscillator

Even though this relationship is based on idealized values, some important parameters can be derived for the design of VCOs. The Q of the loaded resonator directly affects the phase noise. For this reason, coaxial resonators must be used in the case of very low phase noise requirements. Low noise oscillators require components with a low corner frequency of the flicker or l/f noise; therefore, bipolar transistors are normally used in VCOs instead of FETs. Components based on GaAs are not well suited as their noise edge is significantly higher than that of the silicon transistors.

The noise figure F of the oscillator, which is internal to the switching, depends not only on the noise figure of the active component, but also on the switching configuration. The power output setting of the oscillator also influences the noise. However, the oscillator's current consumption must not be neglected.

One very important point that is not taken into consideration in Equation 8 is a clean voltage supply. Significant fluctuations can occur in the voltage supply, particularly through the end stage. Unwanted modulation side bands, which lie outside the loop bandwidth of the PLL switching operation, are produced from the fluctuations in the bias voltage at the modulation input of the VCO.

Tuning sensitivity describes the tuning frequency range as a function of the tuning voltage at the varactor input. The tuning sensitivity depends on the available capacity variation and is inversely proportional to the loaded Q of the resonant circuit. However, frequency dependency of the tuning sensitivity also must be borne in mind. If the frequency dependence is too great, then the performance of the synthesizers is adversely affected.

Load pulling describes the sensitivity of the free-running VCOs to load fluctuations at the VCO output. This load pulling is specified for a mismatched load with a defined SWR (for example, SWR = 2.0) where the phase angle can lie between 0° and 360°. At its simplest, this requirement may be achieved using an additional buffer amplifier. Such a buffer amplifier also improves the output power level of the VCO, which must supply the RF scaler of the PLL synthesizer in addition to a pulsating stage. However, a buffer amplifier increases the current supply of the VCO. Load pulling of the transmitter branch VCO is particularly critical due to the last stage and its load.

 

CONCLUSION

This article has presented the fundamentals for the design and use of VCOs. From what has been said, it is clear that the VCO, together with the PLL, represents an elementary unit that makes an important contribution to the design of a base station. Therefore, it makes sense that the manufacturers of VCOs are also involved in the production of suitable PLL components, and it is conceivable that both VCO and PLL modules could be integrated into one case.

References

1. Hans Lobensommer, Die Technik der modernen Mobilkommunikation (The Technology of Modern Mobile Communications), Franzis-Verlag.

2. Heinz Preibisch, GSM Mobilfunk: Übertragungstechnik (GSM Mobile Radio Transmission Technology), Schiele & Schön, 1994.

3. J.W. Boyles, "The Oscillator as a Reflection Amplifier: An Intuitive Approach to Oscillator Design," Microwave Journal, Vol. 29, No. 6, June 1986, pp. 83&ndash;98.

4. Frank Baberg, Kapazitive Bauelemente für Hochfrequenzapplikationen (Capacitive Components for Radio Frequency Applications), HF Report, May 2/99.

5. Microwave & RF Devices, Ceramics and Capacitors, Time and Frequency Products Catalogue 2000, issued by Tekelec Temex S.A., Montreuil.

6. D.R. Leeson, "A Simple Model of Feedback Oscillator Noise Spectrum," Proceedings of the IEEE, 1966, pp. 329&ndash;330.

7. Ulrich Rohde and Frank Hagemeyer: "Feedback Technique Improves Oscillator Phase Noise," Microwaves & RF, November 1998.

8. Wolf Dieter Schleifer, Hochfrequenz-und Mikrowellen-Me?technik in der Praxis Radio Frequency and Microwave Measurement Techniques in Practice, Hüthig.