DC and Pulsed IV Characteristics of GaAs MESFET Devices
New measurement procedures using a DC and pulsed IV characterization system illustrate the significant effect that the thermal and frequency dispersion phenomena in GaAs MESFETs have on the IV characteristics of the device. The new procedures presented enable the effects of self-heating and frequency dispersion and the interaction between the two to be observed independently.
J. Rodriguez-Tellez
University of Bradford
Bradford, West Yorkshire, UK
T. Fernandez, A. Mediavilla and A. Tazon
University of Cantabria
Santander, Spain
The characterization of GaAs MESFET and HEMT devices under pulsed conditions1,2 has been used extensively during recent years. This measurement idea was originally proposed because it enables the self-heating effect to be controlled. However, interpretation of the resulting data from such measurement systems is not as straightforward as it may appear. The complex interaction between self-heating and the frequency dispersion effect, which is temperature, frequency and electric field dependent, is usually not considered fully. In this article, a variety of IV measurements carried out under DC and pulsed conditions illustrate the strong influence of frequency dispersion and self-heating on device characteristics. The proposed measurements enable these two effects to be considered separately.
Measurements
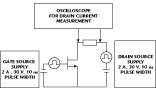The measurement system employed to investigate the frequency dispersion and thermal effects in GaAs devices is shown in Figure 1 .3 Under software control this system enables both static and pulsed IV measurements to be performed as well as pulsed measurements from different static points.
Static IV measurements can be performed over a 0 to 30 V voltage range, and large power devices can be accommodated since each DC supply is capable of delivering 2 A. A user-defined delay time can be used to control the time (after the DC bias voltages are applied and before the drain current is measured). This feature is useful in assessing the self-heating effect from a DC point of view.
Pulsed IV measurements also can be performed over a 0 to 30 V voltage range with current levels of up to 2 A. The pulsed measurements are performed by pulsing the drain source and gate source terminals, pulsing only the gate source terminal while the drain source terminal is swept in a DC manner and pulsing only the drain source terminal while the gate source is swept in a normal DC manner. From a thermal point of view these three situations are the same provided the device is, from a static point of view, pinched off. However, as will be demonstrated, these three cases produce dynamic characteristics that are quite different.
A pulse width of 1 ms with a repetition rate of 1 ms was employed for the results presented in this article. For the MESFETs considered this pulse width is sufficiently short to ensure that no significant self-heating takes place.2 The 1 ms period also corresponds to a measurement frequency after the frequency dispersion effect has taken place. For the devices considered here, the dispersion effect was found to be pronounced in the 40 to 800 Hz region. In this frequency range, the variation of the drain-source resistance with frequency resembles the frequency response of a lowpass filter.4-6 Beyond 800 Hz the device remained dispersive; however, this dispersion was found to be to a much lesser extent and remained reasonably constant over a broad frequency range.
The pulsed measurements described previously can be performed with the device biased from a static point of view at any user-defined position. This measurement procedure enables the self-heating arising from the static bias and its subsequent effect on the dynamic characteristics to be investigated. However, this procedure is not particularly useful from the point of view of observing the dispersion and thermal effects independently. It is also worth bearing in mind that the pulses generated to measure the dynamic characteristics can be positive, negative or zero depending on the static point selected and the dynamic bias point to be measured. This point is important since it has a bearing on the self-heating and frequency dispersion effects.4
The three described basic measurements and the conditions specified are by no means an exhaustive list of the capabilities of the measurement system. However, the results presented in this article only utilize these three simple techniques.
Devices Considered
In order to describe the general findings of this work, a 900 mm gate-width (four fingers with 225 mm gate width per finger), -0.8 V pinch-off voltage, 0.5 mm gate-length ion-implanted GEC Marconi Materials Research Ltd. MESFET is used as the demonstrator. Extensive thermal data concerning this and the other devices considered from a static point of view have been published previously.7 Although similar trends in the measured data were observed with the other devices considered, interesting differences were discovered. These results were not unexpected since the device design (such as number of fingers, gate width and pitch between fingers) has a significant bearing on its thermal properties, which, in turn, modify the dispersive qualities of the device. However, this aspect is outside the scope of this article and the behavior reported here is generally true of the other devices.
Self-heating Due to Static Bias
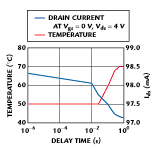The measured DC drain current of the device at Vgs = 0 V and Vds = 4 V as a function of delay time is shown in Figure 2 . Even after the static bias is allowed to settle for one second, the drain current is not unduly smaller than when a faster acquisition time is employed. For delay times shorter than 10 ms, the drain current is not significantly affected. This result is in keeping with the observations of others1,2,8 who have shown MESFETs to take a relatively long time before the self-heating effect has a significant impact on the IV characteristics of the device. At the bias point selected the temperature of the device was determined to be 70ºC with the use of liquid crystals.
DC measurements performed at other bias points not unexpectedly also showed a relatively small change in the IV characteristics as the delay time was varied in the microsecond to millisecond range. The temperature of the device clearly varied as the power dissipated varied. For this device the thermal impedance was measured to be 125ºC/W.
Self-heating Due to Pulsed Bias
As a check on the self-heating issue considered previously, the drain current of the device was monitored with an oscilloscope as the drain source and gate source junctions were pulsed from the static point of Vgs = -1 V, Vds = 0 V to the dynamic point of vgs = 0 V, vds = 4 V. In this test the period was set to 0.1 s (10 Hz) to ensure that the frequency dispersion effect did not affect the measured data. This condition was confirmed by comparing the dynamic and static values of the drain current. With this period the pulse width was then increased from 10 ns until the self-heating had a measurable effect on the drain current. This point was determined to be when a pulse width of 10 ms was employed, which agrees with the earlier measurement.
Therefore, the use of a pulse width of 1 ms in order to measure the dynamic characteristics of the device seems appropriate as a means of eliminating the self-heating effect. This issue should be reconsidered for other GaAs devices such as HEMTs and HBTs since the thermal time constant of these devices may be faster. The period or measurement frequency also should be selected to ensure that the self-heating effects are eliminated. The use of 1 kHz seems appropriate for the MESFETs considered here. This frequency also ensures that the dynamic IV characteristics measured correspond to a frequency point after the dispersion effect has settled. The employment of different measurement frequencies is useful if the area where the device is strongly frequency dependent is to be observed.
Dynamic Characteristics
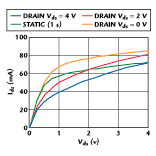
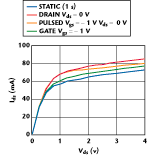A variety of curves measured under static and pulsed conditions are shown in Figure 3 . For the pulsed cases a pulse width of 1 ms with a period of 1 ms was employed. For the static curve a delay time of 1 s was used to ensure a stable self-heating temperature. All of the curves correspond to the vgs (or Vgs ) = 0 V case.
Curve 1 corresponds to the case where the drain source is pulsed from the static point of Vds = 0 V while the gate source is maintained at Vgs = 0 V (static). Curve 2 corresponds to the case where the gate source is pulsed from the static point of Vgs = -1 V while the drain source is swept in a normal DC manner. Curve 3 corresponds to the case where the gate source and drain source junctions are pulsed from the static points of Vgs = -1 V, Vds = 0 V. From a thermal point of view these three pulse cases are the same. Since the device is, from a static point of view, in the off state, the ambient temperature and the pulse parameters are the same. It should also be remembered that the drain source resistance of the device is high (> 10 kW) when it is pinched off. If the intention is to ensure that no self-heating takes place, it is not necessary to pulse the gate and drain terminals. However, this facility does lead to interesting behavior as demonstrated in the data.
If it is accepted that for the pulsed curves the ambient and any self-heating temperatures are the same, then it follows that the differences between curves 1, 2 and 3 are due to frequency dispersion effects. Bearing in mind the previous results obtained with the DC measurements, the difference between curve 2 and the DC curve is due to thermal (approximately 1 mA) and frequency dispersion effects. Even if this difference was entirely due to thermal effects, it is still considerably smaller than the differences observed between the pulsed curves.
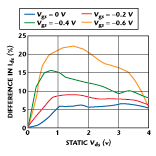
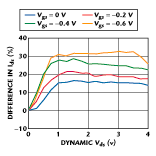The presentation of the data as shown in the graph, while interesting, can lead to the erroneous conclusion that frequency dispersion effects are not relevant in the linear region. Figures 4 and 5 show the same information but it is expressed as the percentage difference in the drain current between the static and the pulsed curves. Note that the dispersion effect increases as the gate source voltage becomes more negative and, therefore, the drain current in the device decreases. The data plots illustrate quite well the dependence of the dispersion effect on electrical field and reinforce the fact that it is not a thermal effect, which would have the opposite effect. Note also that pulsing the gate or drain produces a similar percentage difference in the drain current for the same change in the electric field. Also notice the almost linear dependence of the dispersion effect on electric field in the linear region.
Dynamic Behavior from Different Static Points
Of course, the pulse measurements can be performed with the device biased from a static point of view at any point. Doing so means the amount of self-heating can be controlled and its effect on the dynamic characteristics observed. Figure 6 shows the response of the device for the Vgs = 0 V pulse case when the Vds static point is varied. The DC curve is superimposed for comparison purposes. The drain-source terminal is pulsed and the gate-source junction is kept at a fixed potential of 0 V only for the pulsed curves.
The pulsed measurements are performed for the case where the static value of Vds is 4 V using negative pulses of 1 ms width with a period of 1 ms. This curve corresponds to the device at its hottest point because of the DC power dissipated. Since it has been previously demonstrated that a 1-ms-wide positive-going pulse is incapable of causing any significant self-heating, it follows that a 1-ms-wide negative-going pulse is unable to cool down the device. Therefore, from a thermal point of view, the device is at a constant temperature corresponding to the power dissipated at Vds = 4 V. The same is true for the Vds = 2 V curve where no additional heating is introduced above 2 V (positive-going pulses). Below 2 V (negative-going pulses), the device temperature corresponds to the power dissipated at 2 V.
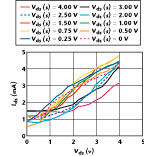While demonstrating that by altering the static bias the characteristics of the device are changed, the presented data should be viewed with caution. It would be incorrect, for example, to assume that the differences between the pulsed curves are entirely due to self-heating effects. Certainly by adjusting the static bias the self-heating has been altered, but by doing so the dispersion effect has also been modified. This complication arises not just because of the dependence of the dispersion effect on temperature but also because of its dependence on electric field and frequency. As shown in Figure 7 , the same experiment was repeated, but this time the gate-source voltage was fixed at -0.8 V, which is very close to the pinch-off point of the device. Here the DC power dissipated and, thus, the self-heating effects are small, yet the changes between the pulsed curves are quite large. This result is in keeping with the results presented in the previous section.
The grouping of the displayed curves is worthy of attention. In the middle of the saturation region (for example, Vds = 2.5 V), all the curves measured with static values less than 2 V are grouped. At this vds point the dynamic values of the curves are measured with positive-going pulses. Then there is a large gap and all the curves measured with static values greater than 2 V are grouped. At this vds point the dynamic values of the curves are measured with negative-going pulses. The eye, or area in the middle of the saturation region where none of the curves cross, is clearly evident. The grouping and crossover of the curves as vds varies illustrate the dependence of the dispersion on electric field and self-heating.
The lack of an eye from the characteristics shown in the previous data plot is believed to be a result of the increased temperature caused by the self-heating. This condition, combined with the change in the biasing conditions, obscures the hysteresis effect. For example, this particular device’s frequency dependency was found to be at its strongest between the temperature range of -50º and +220ºC. Outside of this temperature range the device exhibited frequency-independent IV characteristics.4
While appearing attractive, the previous measurements, where the pulse and static conditions are varied in order to modify the self-heating effect, provide data that are difficult to interpret because of the variables involved. Of these variables, the dependence of the dispersion effect on electric field is the most difficult to quantify in a meaningful form for modeling purposes. Performing pulse measurements with the device biased from a static point of view in the off state in a temperature-controlled chamber provides certain advantages. For example, the IV characteristics can be observed over a wider temperature range and the resulting change to the dynamic characteristics can be unmistakably attributed to such a temperature change. However, the dependency on electric field remains difficult to quantify unless the off state of the device is used as a reference point. This aspect is currently under consideration and will be reported upon at a later date.
Conclusion
A measurement system for observing the dependency of the device IV characteristics on frequency, electric field and temperature has been presented. The system uses pulse generators and DC power supplies to enable the gate source, drain source or both junctions to be pulsed from any static point. Results presented show the strong dependence of the device’s dynamic IV characteristics on frequency dispersion effects and how this dependence is modified by thermal effects caused by the power dissipated in the device.
Acknowledgment
The authors would like to thank the Spanish Ministry of Education and Science for its financial support of this work under the Acciones Integradas programme.
References
1. A.E. Parker and J.B. Scott, “Method for Determining Correct Timing for Pulsed I/V Measurement of GaAs FETs,” IEE Electronic Letters , Vol. 31, September 1995, pp. 1697-1698.
2. J.P. Teyssier, P. Bouysse, Z. Ouarch, D. Baratand, T. Peyretaillade and R. Quere, “40 GHz/150 ns Versatile Pulsed Measurement System for Microwave Transistor Isothermal Characterization,” IEEE Transactions on Microwave Theory and Techniques , Vol. 46, No. 12, December 1998, pp. 2043-2052.
3. T. Fernandez, Y. Newport, J.M. Zamarillo, A. Mediavilla and A. Tazon, “High-speed Automated Pulsed IV Measurement System,” 23rd European Microwave Conference Proceedings , Madrid, September 1993, pp. 494-496.
4. J. Rodriguez, B.P. Stothard and M. Al-Daas, “Static Pulsed and Frequency Dependent IV Characteristics of GaAs FETs,” IEE Proc. Pt. G , Vol. 1243, No. 3, June 1996, pp. 129-133.
5. J. Rodriquez, B.P. Stothard and M. Al-Daas, “Frequency and Temperature Dependency of Output Conductance of GaAs FETs,” Microwave Journal , Vol. 38, No. 8, August 1995, pp. 88-94.
6. J.M. Colis, M.G. Miller, G.N. Maracas and D.A. Johnson, “Frequency-dependent Electrical Characteristics of GaAs MESFETs,” IEEE Trans. ED , Vol. 37, No. 5, May 1990, pp. 1217-1227.
7. J. Rodriguez, S. Laredo and R.W. Clarke, “Self-heating in GaAs FETs -- A Problem?” Microwave Journal , Vol. 37, No. 9, September 1994, pp. 76-92.
8. J.A. Higgins, “Thermal Properties of Power HBTs,” IEEE Trans. ED , Vol. 40, No. 12, December 1993, pp. 2171-2177.
J. Rodriguez-Tellez received his BSc, MPhil and PhD degrees in electrical engineering in 1979, 1982 and 1985, respectively, from Leeds and Bradford Universities, UK. He is also a Chartered Engineer (C. Eng.) and a European Engineer (Eur. Ing.). From 1979 to 1983, Rodriguez-Tellez worked for Standard Telecommunications Laboratories, Harlow, UK, as a research engineer in high speed communication systems. Since 1983, Rodriguez-Tellez has worked in the electronic and electrical engineering department at the University of Bradford, where he is currently a reader in solid-state devices. His research interests include Si and GaAs devices, interconnects and package modeling for microwave circuit applications.
Tomas Fernandez Ibanez received his PhD in physics from the University of Cantabria, Spain in 1996. Since 1998, he has been an assistant lecturer in the department of communications engineering at the University of Cantabria. His research interests include large-signal, nonlinear modeling of III-V compound transistors and SiGe devices.
Angel Mediavilla Sanchez graduated with honors in 1978 and received his PhD degree in physics in 1984, both from the University of Cantabria, Spain. From 1980 to 1983, he was ingenieur stagiere at Thomson-CSF, Corbeville, France. Currently, Mediavilla is a professor in the department of communications engineering at the University of Cantabria. His research interests include the simulation of devices and circuits using GaAs technology and its application in computer-based design.
Antonio Tazon Puente received his PhD degree in physics from the University of Cantabria, Spain in 1987. Since 1991, he has been a professor at the University of Cantabria, first in the department of electronics engineering and currently in the department of communications engineering. Tazon’s research interests include the modeling of GaAs and SiGe devices from a linear and nonlinear point of view.