Static Fractional: The True Fractional Division Method of Indirect Synthesis
A significant development of the indirect frequency synthesis method, called fractional-N, has been developed recently. This article shows that this dynamic method is only one of two possible ways for the implementation of the fractional division idea. The second method supplies fractional division statically. Various realization possibilities of that second method are also described, as well as their advantages and disadvantages with reference to the first method.
Stanislaw Alechno
WZR RAWAR
Warsaw, Poland 
The first indirect frequency synthesis method, the dynamic method, identified up to now simply as fractional-N, is used here as a reference for the second method. In some sense, the dynamic method's name is opposite to the technique's actual operation. Figure 1 shows the method's principle in a simplified way.
There are many implementations of this technique.1-7 However, circuits are usually complex and descriptions are rather difficult. Here, the essential, simplified model identifies some of the basic properties. The dual-modulus divider is an essential and well-known element of the circuit often used in microwave synthesizers. In a typical application it is a component of the pulse-swallow counter in which a dual-modulus prescaler of the N/(N + 1) type (for example, 5/6, 10/11 or higher) is arranged, together with two programmable counters controlling its state and determining how many counts by N and N + 1 will be in an output cycle. The control counters count the pulses from the prescaler, producing an output pulse after a two-part period. Each programmed part is relevant to the given modulus state. In effect, the arrangement yields continuous division programming. On the whole, this type of circuit makes a normal, although complex, unity step programmable divider with the advantage that only the dual-modulus prescaler, usually a high frequency device, works at the high input frequency. Other logic circuits operate at a much lower frequency.
The way in which a dual-modulus divider is used in the circuit and its purpose are completely different. On one hand, the divider's implementation is simpler, directly driving the phase detector and not the control counters (although an irrelevant, following divider may exist). On the other hand, the purpose appears to be strange, hindering the normal work of the phase-locked loop (PLL). The division of the dual-modulus divider is altered periodically, which means that the effective frequency division in the feedback loop is changed dynamically in time, contrary to the pulse-swallow counter. The output pulse rate now has additional periodicity. Therefore, the phase detector receives a signal with its frequency varying in time and produces a correspondingly variable output signal that modulates the VCO. The effective fractional value of frequency division is obtained here dynamically, that is, by time averaging the N and N + 1 divisions. The division value depends on the durations of the divider's states. The overall division factor is accomplished by averaging the phase detector signal in the loop filter. Note the opposing terms static and dynamic are sometimes used with microwave frequency dividers to distinguish the circuit's resistance and susceptibility to self-oscillation. Obviously, this is a completely different matter and requires a different use of these terms.
As is apparent, this simple idea has an obvious drawback: The average value of the output frequency is adequate, but because the phase detector output voltage in such a circuit has a variable component, some relevant spurious signals will appear in the output spectrum. The simplest way to limit this effect is to narrow the loop filter bandwidth properly. However, the bandwidth increases proportionally to the synthesizer switching time. Such a solution is utilized in simple circuits with low fractionality (the ratio of the phase detector comparison frequency to the available synthesis step). In the fundamental PLL, this ratio amounts to unity. An efficient, although complex, solution is to compensate for the variable component at the phase detector output. The signal required for this purpose can be derived from the circuit controlling the dual-modulus divider. Typically, that function is accomplished using an accumulator (an adder with a latch in the loop) by modifying its state by an assumed value with the clock rate and switching the dual-modulus divider by the overflow signal. The increasing digital signal in the accumulator corresponds to the sawtooth signal of the phase detector. Therefore, after transformation in a digital-to-analog converter and phase inversion, the signal from the accumulator can be added to the phase detector signal to compensate for the variable component.
Additional specific applications of the dynamic fractional-N PLL have been developed with the purpose of canceling spurious sidebands, an inherent contaminant of dynamic fractional division.4 Synthesizers utilizing this idea offer broad possibilities, yet their implementations are complex. Specialized ICs that have appeared during the last few years are not numerous and are limited in their capabilities.5,6
As indicated previously,1 fractional-N is not a correct name for the method presented because real fractional division is not performed, but rather periodically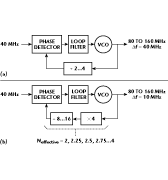 
changing division. This dynamically changed frequency division2,3 results in the dynamic working of the PLL circuit. Therefore, the term dynamic fractional-N is more appropriate, particularly since there are possible realizations of true static fractional divisions. Static fractional division consists of a frequency multiplier and a programmable frequency divider with unity steps, as shown in Figure 2.
The fundamental indirect synthesis circuit is shown with a reference frequency of 40 MHz, which gives synthesis steps (channel spacing and resolution) of the same value. An increase in resolution would require a decrease in the phase detector comparison frequency and an increase in the frequency divider division factor in the feedback loop. In turn, these factors cause a degradation of essential synthesizer parameters, that is, switching time and phase noise. Various kinds of complex indirect synthesis circuits have been generated to counteract that fundamental indirect synthesis circuit disadvantage. Fractional division is one effective way to nullify the disadvantage, allowing small synthesis steps without worsening the essential device parameters. The synthesis step can be lowered to 10 MHz by increasing the division factor of the programmable frequency divider by a factor of four. Because the divider is programmable with a unity increment, the number of channels increases simultaneously; the ´4 multiplier restores the primary range of division in the feedback loop, resulting in increased resolution.
It should be noted that the idea of static fractional-N is satisfied either with the multiplier placed before or after the divider. This optional multiplier placement offers two different variants of the methods presented, each having its own advantages and drawbacks. When placed before the frequency divider, the multiplier must be suitably broadband. Standard, broadband, integrated frequency doublers (manufactured by many companies) are particularly suitable here, allowing wideband multiplication by 2, 4, 8 and beyond.
The advantages of the second variant, with the multiplier after the divider, are lower requirements for the maximum operating frequency of the divider, as well as a lower, steady-state multiplier operating frequency. A disadvantage of this variant is an increase in the frequency divider's phase noise level resulting from the multiplication, which may influence the total phase noise of the synthesizer.
Standard, programmable synchronous counters produce narrow output pulses with a duration equal to the input signal period. These spikes have a spectrum rich in harmonics, therefore, the multiplying function can be accomplished by filtering a desired harmonic. This type of circuit may operate unreliably during switching because of possible synchronization on an undesired harmonic. This method requires presteering of the VCO or an additional circuit to help lock on the proper frequency.
The problems with switching could be avoided by applying a broadband multiplier. Yet, in this case, application of broadband frequency multipliers is difficult because of the pulsed input signal. When dealing with a pulse signal, there are various kinds of pulse-multiplying circuits that may be sufficiently broadband, yet such circuits are difficult to realize, especially at high frequencies. This type of application, consisting of the generation of additional pulses with the help of delay circuits, has been described previously,8 but is a rather complicated solution involving possible undesired signals in the output signal spectrum resulting from delay circuit variations.
The fractionality obtainable in various applications of the static fractional-N method is limited by frequency multiplication realization. In the simplest circuits, the multiplication is limited to approximately 10. The static method has found little use in signal synthesizers where the dynamic fractional-N method has been used for a long time, making high values of fractionality possible. But in applications that do not require small tuning steps (for example, in radars), the static method can be effective. In such applications, a high reference frequency (40 MHz) is needed to assure low switching time in a high performance frequency synthesizer for a radar application (for example, < 5 ms for 0.1¡ phase setting). At the same time, the required synthesis step is 10 MHz, a typical value for a radar system. As can be seen, the fundamental indirect synthesis circuit is not sufficient here, while application of the static fractional-N method is satisfactory. The configuration using a multiplier can be transformed to a microwave synthesizer by inserting a microwave VCO and a mixer in the feedback loop, accomplishing suitable frequency conversion. This configuration is efficient in lowering the phase noise level.9 As a result, the method presented is a simple and effective way to achieve small switching time and low phase noise simultaneously - two essential parameters of a high performance microwave frequency synthesizer.
References
1. U.L. Rohde, Digital PLL Frequency Synthesizers, Theory and Design, Prentice-Hall, 1983.
2. B.G. Goldberg, Digital Techniques in Frequency Synthesis, McGraw-Hill, 1996.
3. R. Hassun, "The Common Denominators in Fractional-N,"Microwaves & RF, June 1984.
4. B. Miller, "Technique Enhances the Performance of PLL Synthesizers," Microwaves & RF, January 1993.
5. W.S. Djen and D.J. Linebarger, "Fractional-N PLL Provides Fast, Low Noise Synthesis," Microwaves & RF, May 1994.
6. J. Stilwell, "A Flexible Fractional-N Frequency Synthesizer for Digital RF Communications," RF Design, February 1993.
7. T. Nakagawa and T. Tsuhakara, "A Low Phase Noise C-band Frequency Synthesizer Using a New Fractional-N PLL with Programmable Fractionality," IEEE Transactions on MTT, February 1996.
8. T. Nakagawa and T. Ohira, "A Phase Noise Reduction Technique for MMIC Frequency Synthesizers That Uses a New Pulse Generator LSI," IEEE Transactions on MTT, December 1994.
9. G. Morris, "Microwave Indirect Synthesis," Microwave Engineering Europe, August/September 1991.
Stanislaw Alechno received his MSEE degree from the Warsaw University of Technology (Poland) in 1988. After graduation, he worked for WILMER, the microwave instruments establishment of the Polish Academy of Sciences, and then for LAMINA, the electron components establishment. Currently, Alechno is employed as a microwave and RF design engineer at WZR RAWAR. His main area of activity is microwave frequency synthesis.