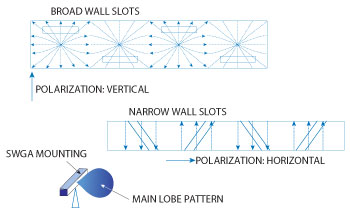
Figure 1 The choice of slot position affects the polarization of the fields. The dashed lines depict the peak currents that flow on the walls for the standing wave TE10 condition.
Slotted waveguide antennas (SWA) are often employed in radar applications where design specifications commonly require high gains and mechanical robustness. Since the peak power transmitted by radar antennas is usually very high, waveguide antennas present a practical alternative to planar arrays. While numerous design references and guidelines exist for planar arrays, there are far fewer for slotted waveguide antennas. This article presents a comprehensive workflow for the analysis and design of a slotted waveguide antenna with slots placed on the narrow wall of the waveguide. The virtual design is modeled and simulated using two different numerical methods and different mesh types. This simulation is compared to the analytical solution for array antennas and to the performance of a physical prototype.
Radar is an essential, safety-critical component of modern navigation and radar antennas need to be designed to exacting specifications. Not only do the antennas used on mobile platforms such as ships need to be high gain with tightly-controlled beamwidths, they also need to be strong, compact, lightweight and resistant to the effects of roll and motion. Slotted waveguide antennas can fulfill all of these criteria.
As the name suggests, slotted waveguide antennas consist of lengths of waveguide with slots milled into their conducting walls. These slots introduce discontinuities in the conductor and interrupt the flow of current along the waveguide. Instead, the current must flow around the edges of the slots, causing them to act as dipole antennas.1,2
The two basic types of SWAs are standing wave and traveling wave. In a traveling wave SWA, the waveguide is built with matched loads or absorbers at the end, while in a standing wave SWA, the end of the waveguide is short-circuited. The short is usually placed at a quarter of the guided wavelength (λg) after the last slot so that it behaves as an open circuit to the last slot. Standing wave slotted waveguide antennas are resonant structures and, therefore, have narrower bandwidths, but in general they are easier to fabricate than traveling wave antennas.
Depending upon the desired field polarization, the slots can be placed on either the narrow or broad wall of the waveguide, as shown in Figure 1. At the fundamental TE10 mode, longitudinal slots on the broad wall will produce a field with vertical polarization, while transverse slots on the narrow wall result in a horizontal field polarization. For each design, the polarization depends on the specific antenna use.
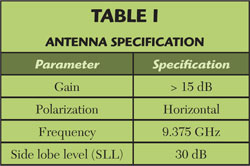
Figure 2 Edge-slot transmission line circuit model.
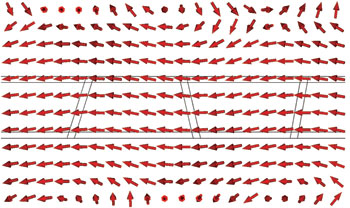
Figure 3 Vertical E-field component spatially cancelled, resulting in a horizontally polarized wave over the azimuthal plane.
To demonstrate the applicability of 3D simulation to SWAs, this article describes the design of a naval radar antenna. The specification requires that the antenna operate in X-Band (8 to 12 GHz).3 The scanning beam must have a narrow beamwidth in the azimuth plane and a wider beamwidth in the elevation plane to compensate for the roll of the ship. Other parameters are specified in Table 1.
These requirements can be fulfilled by the arrays in Figure 1, with the horizontal polarization requirement determining the use of the narrow wall slots. In order to achieve a resonant length, narrow wall slots must penetrate into the upper and bottom broad walls. These slots are known as edge-slots. Figure 1 shows these slots running diagonally between the broad walls. If they were perfectly perpendicular, they would not radiate, since the slots would run parallel to the current lines and therefore would not interrupt the current flow. By tilting the slots, a fraction of the current lines are interrupted, causing the slots to radiate. Figure 2 shows the edge-slot construction and its circuit representation. The slot has a characteristic admittance which can be broken down into contributions from the conductance (G) and the susceptance (B).
For the design shown in Figure 1, adjacent slots have opposite inclinations so that the vertical components from these slots are cancelled out in space, as shown in Figure 3. This improves the spectral purity of the transmitted waves.
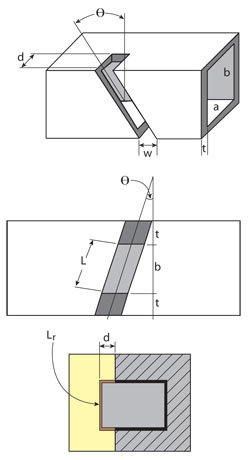
Figure 4 Geometric parameters for the edge slots.
Array Design
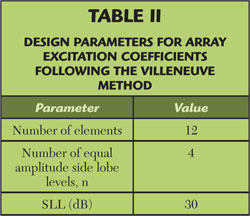
The slots are distributed along the waveguide so that they form an array; the choice of array type and its setup allow the engineer to specify the gain, side lobe level (SLL) and beam steering. The discrete Taylor distribution4 was chosen for the array, since it produces a good theoretical match to the SLL requirement as well as providing a smooth variation between the excitations of adjacent elements – a useful characteristic when mutual coupling is a concern.
Because this is an SWA, the waveguide hosts a standing wave, in which slots are placed at the antinodes – locations where the electric field reaches its maximum. They are therefore separated by half of the guided wavelength (λg/2). Since a half wavelength on the Smith chart corresponds to a complete rotation, the individual slot admittances are summed at the waveguide input as if they were at the same position.
SWA designs do not usually take into account mutual coupling between slots.5 Since mutual coupling and waveguide thickness have a significant influence on the admittances of the edge-slots, an accurate analysis of the antenna should take their effects into account. Electromagnetic (EM) simulation can model both these effects, as well as the effects due to coaxial transitions and flanges. With EM simulation, the traditional empirical trial-and-error method is replaced by a computational evaluation.
The procedure assigns a theoretical excitation distribution to the array, where each element coefficient corresponds to a slot conductance (at the central frequency where the susceptance is zero) ensuring the length of each slot corresponds to a resonance at the operational frequency.
The first step characterizes the individual slots. Figure 4 shows the important parameters.
The choice of waveguide (WR-90) and milling equipment determines the parameters a = 22.86 mm, b = 10.16 mm, w = 1.59 mm and t = 1.27 mm. This leaves only two independent parameters to optimize: Θ (slot inclination angle) and d (depth of the slot). The complete slot length is assumed to be the one measured on the internal face of the waveguide, parameter Lr, with a resonant length Lr = 0.4625 λg.6
Evaluation of the Resonant Parameters Θ and Lr
For each slot, the first value to be found is the slot resonant length (Lr,i) for a given slot inclination (Θi). Since mutual coupling must be taken into account, small variations from the initial Lr value are expected. If the final antenna has N slots, an array of N identical slots is simulated for each angle. This is more realistic than a single slot simulation, since it considers the effect of mutual coupling. Figure 5 shows the equivalent circuit model of a generic SWA. Note that a displacement of λg/2 in a lossless transmission line corresponds to the same point on the Smith chart, so that the resultant admittance measured at the first slot, Yin, is equivalent to the sum of all the admittances.
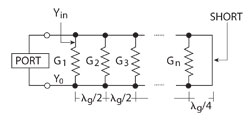
Figure 5 Equivalent circuit model for the resonant SWA.
A parameter sweep using the frequency domain solver (F-solver) of CST MICROWAVE STUDIO®7 is carried out for each angle (Θ), adjusting the slot depth (d) to find the slot’s resonant length (Lr). The resonance is found for the single slot when the normalized susceptance (b) of the de-embedded waveguide port to the center of the first slot is null. We can assume that the computed admittance at the waveguide port is the product of the number of slots and the normalized slot admittance.
At the end of this process two curves are derived: slot inclination versus required slot conductance, and slot resonant length versus slot inclination. These curves are the design curves used in the synthesis of each slot in an N edge-slotted waveguide antenna.
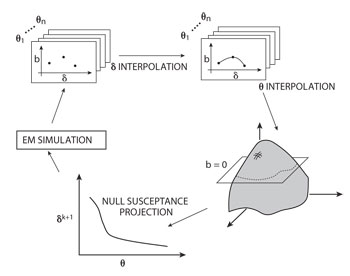
Figure 6 Interpolation routine implemented as a search routine for the best parameters that generate a null susceptance slot.
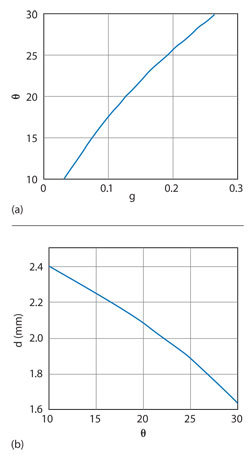
Figure 7 Design curves for an edge-slotted waveguide antenna with 12 elements.
Evaluation of the Null Susceptance Curves
The parameter sweep returns a set of admittance points that must be evaluated in order to determine the optimum geometrical parameters to achieve null susceptance. For that we use an interpolation routine implemented in MATLAB, as illustrated in Figure 6. At first, the points of susceptance as a function of the slot length (here δ is used as a tweaking coefficient for Lr) are interpolated using the interp1 function with pchip method for each angle, and then the curves are interpolated in Θ using the interp2 function with the cubic method. This builds up a susceptance surface. The slice of null susceptance (b50) is derived by using the function contourc. The curve described by this contour contains the values of Lr (Θ) required for resonance. These are then inserted back into the 3D model, and the antenna is re-simulated. This process is repeated until the desired accuracies are achieved. Figure 7 shows the design curves for a 12-slot antenna. These curves allow the engineer to carry out antenna array synthesis.
Antenna Synthesis
The antenna synthesis procedure starts with the Taylor polynomial that represents the array function: parameters such as the SLL, the number of elements and the number of side lobes are the inputs, and the outputs are the slots’ individual excitations (an). The curves generated in MATLAB are then examined in order to determine which Θ and Lr will eventually generate the required conductance. Table 2 summarizes the input parameters for the synthesis polynomial.
The next step is the evaluation of the required admittances for the final antenna, considering each element’s excitation. The required normalized conductances (gn) are derived using these equations.
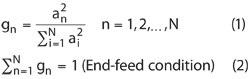
With the design curves in Figure 7, the inclination and resonant length of each slot are determined. Table 3 summarizes the final antenna parameters.
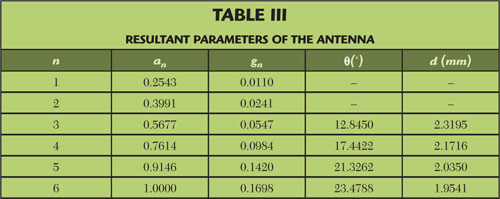
By symmetry, the parameters of the rest of the slots are the same as those of the first half, but in reverse order. Note that the first two elements, and therefore the last two elements, require conductances that are out of the design curve range. In those cases, the lowest inclination is adopted: slots with 10° tilt that are 2.4044 mm deep.
Complete EM Simulation
The antenna design is then evaluated within CST STUDIO SUITE®,7 with the slots filled by a dummy object (made of vacuum). This allows local refinement to be carried out directly on the slot volume, so that convergence is achieved much quicker.
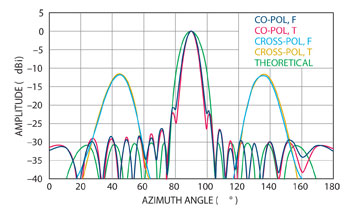
Figure 8 Comparison of the different solver results and the theoretical array factor.
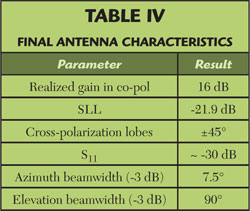
The antenna was simulated with the F-solver, and the simulation was validated using the time domain solver (T-solver). The simulations used adaptive meshing and local mesh refinement over the slots. As shown in Figure 8, the far field results from the F-solver and T-solver agreed closely for both the co-polarization and the cross-polarization. Carrying out two simulations using different numerical methods and meshes helps us confirm the accuracy of the simulation. Table 4 summarizes the antenna characteristics.
The antenna’s maximum gain is 16 dB, and the SLL is –21.9 dB. It is known that the final array radiation pattern is a combination of the pattern of a single radiating element (in this case, a slot), and the array factor (AF). In Figure 8 the theoretical radiation pattern, based on the desired AF, is compared with the simulated complete antennas. Note that the highest simulated side lobe is within the theoretical main lobe, thereby suggesting that it is a modulation of the AF main lobe and not a true secondary lobe. It cannot be mitigated unless the slot geometry is modified.
The array’s actual first SLL is –26 dB. Elsallal et al8 have suggested that due to errors in the phase of the slot excitations, a –30 dB SLL result is not possible in practice. The authors also suggest an optimization technique that modulates the conductance of the slots in order to achieve a simulated –27.3 dB SLL. Since no modulation technique was used, the –26 dB SLL is accepted as an optimum result by the numerical verification of the far field pattern.

Figure 9 Slotted antenna made from a copper WR90 waveguide, top-milled by a CNC machine.
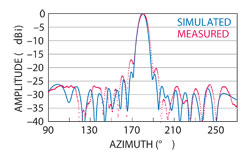
Figure 10 Co-polarization far field pattern results in the azimuth plane (measurement and simulation).
Prototype Measurement
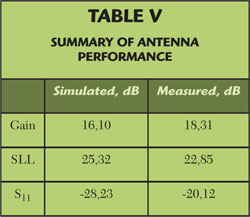
The final antenna, shown in Figure 9, was prototyped and tested in an anechoic chamber. The co-polarization pattern (see Figure 10) shows that this antenna is very directional in the azimuth plane and demonstrates a close agreement between measurement and simulation. Some of the variation between the far field measurements and the simulation may be attributed to the measurement setup. The antenna was attached to a metallic mast, and it is possible that this mast interacted with the fields. The results are summarized in Table 5.
Conclusion
Edge-slotted waveguide antennas are widely used in radar applications where they outperform other types of antennas such as printed arrays. Despite the ubiquity of SWAs, we were unable to find any previous literature describing comprehensive analytical formulations or computer-aided design programs for SWA synthesis. In the absence of design curves or suitable measurement data, the designer usually resorts to empirical methods to optimize the design. The use of modern computer simulation software offers an alternative approach to SWA design.
The workflow proposed in this paper covers the entire antenna project, from slot characterization to physical prototyping of the antenna, and shows how simulation can be used at every step to improve antenna performance. The antenna described in this article has 12 slots. It achieved optimum performance, verified numerically, without any changes needed to further improve the final design. The measurement of a prototype validates the accuracy of the simulation.
Acknowledgment
The authors would like to acknowledge ATMOS Sistemas Ltda. for financing the antenna manufacturing.
References
- C. Balanis (editor), Modern Antenna Handbook, John Wiley and Sons, 2008.
- J.L. Volakis, Antenna Engineering Handbook, McGraw Hill, 2007.
- IEEE Standard 521-2002 - Letter Designations for Radar Frequency Bands.
- A.T. Villeneuve, “Taylor Patterns for Discrete Arrays,” IEEE Transactions on Antennas and Propagation, Vol. 32, Issue 10, October 1984, pp. 1089-1093.
- W. Coburn, M. Litz, J. Miletta, N. Tesny, L. Dilks, C. Brown and B. King, A Slotted-Waveguide Array for High-Power Microwave Transmission,January 2001, available at http://www.dtic.mil/cgi-bin/GetTRDoc?AD=ADA387308.
- D.N. Das, J. Ramakrishna and B.K. Sarap, “Resonant Conductance of Inclined Slots in the Narrow Wall of a Rectangular Waveguide,” IEEE Transactions on Antennas and Propagation, Vol. 32, Issue 7, July 1984, pp. 759-761.
- www.cst.com/Content/Products/CST_S2/Overview.aspx.
- M.W. Elsallal, B.J. Herting and J.B. West, “Planar Edge Slot Waveguide Antenna Array Design using COTS EM Tools,” Proceedings of the 2007 Antenna Applications Symposium, December 2007, pp. 78-89.
Rodrigo Kenji Enjiu received BSc degrees in Science and Technology (2011) and Information Engineering (2012), both at UFABC, Santo Andre, Brazil. He worked at ATMOS Sistemas Ltda., Sao Paulo, Brazil, first as an intern and later as a microwave engineer. In 2013, he joined CST, Darmstadt, Germany as an application engineer.
Marcelo Bender Perotoni received his BSEE from UFRGS, Porto Alegre, Brazil, and his MSc and PhD degrees in Electrical Engineering from the University of São Paulo, Brazil. In 2003 he was a research student at Colorado University, Boulder, USA and in 2006 he undertook a post-doc with TEMF, Darmstadt, Germany. He is currently a professor at UFABC, Santo André, Brazil.
