Excellent oscillator performance can be expensive. Recent publications1-7 describe the design implementation-techniques of low phase noise crystal-oscillator circuits using, high Q-factor, expensive crystal resonators that show inferior phase noise. Fortunately, approaches have been developed8 to design and optimize the performance of voltage-controlled crystal oscillators (VCXO), even those with relatively low-Q-factor resonators, to achieve excellent phase-noise and frequency stability. Novel crystal oscillator circuits are reported, using medium Q-factor and inexpensive crystal resonator, by which the phase noise of the crystal oscillator at close-in as well as far offset from the carrier, can be minimized using self-injection and mode-locking techniques. The CAD simulated and experimental results are presented to validate the proposed methodology.
A typical oscillator consists of a tuned circuit and an active device such as a transistor. Ideally, the tuned circuit provides a high loaded Q, generally from less than 100 for simple circuits to more than 1 million for crystal-resonator-based circuits. Noise arises from the active device as well as from resonator losses. Noise from a bipolar transistor, for example, stems from base and collector contributions and from device parasitic elements, such as the base-spreading resistor. The filtering effect of the resonator tends to remove the device noise, with higher Qs delivering greater filtering effects. The standard Leeson equation relates these noise effects (Equation 11).
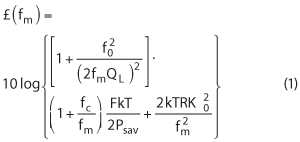
where:
£(fm) = the ratio of sideband power in a 1 Hz bandwidth at fm to total power (in dB); fm = frequency offset; f0 = center frequency; fc = flicker frequency; QL = loaded Q of the tuned circuit; F = noise factor; kT = 4.1 × 10-21 at 300 K0 (room temperature); Psav = average power at oscillator output; R = equivalent noise resistance of tuning diode (typically 50 Ω - 10 kΩ); K0 = oscillator voltage gain.
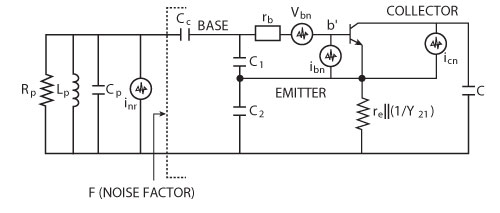
Figure 1 Equivalent configuration of the Colpitts oscillator circuit including noise contribution3.
Equation 1 is limited by the fact that the loaded Q typically must be estimated; the same applies to the noise factor. The following equations, based on this equivalent circuit, are the exact values for Psav, QL, and F, which are required for the Leeson equation. Figure 1 shows a typical simplified Colpitts oscillator circuit for use in providing insight into a novel noise calculation approach. The noise factor can be calculated by:
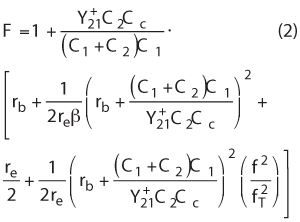
After approximation (simplification in analysis3):
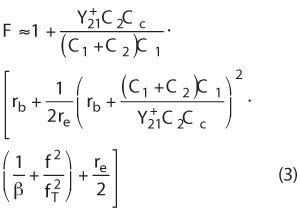
where Y21+ is a large signal Y-parameter for a given oscillator circuit operating condition.
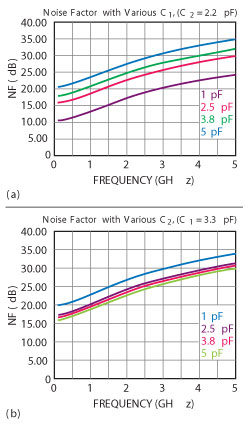
Figure 2 Plot of the noise factor vs. frequency for various values of C1 (a) and C2 (b).
Figures 2a and 2b illustrate the dependency of the noise factor (NF) on the feedback capacitors C1 and C2. From Equation 1, the phase noise of the oscillator circuit can be minimized by optimizing the noise factor terms as given in Equation 3, with respect to the feedback capacitors C1 and C2.
Equation 4 can be found by substituting 1/re for Y21+ (+ sign denotes the large signal Y-parameter)3:
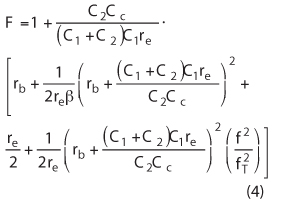
When adding an isolating amplifier, the noise of an oscillator circuit is determined by Equation 5:
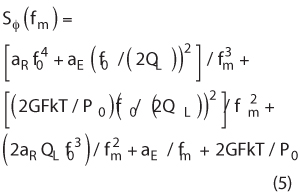
where G = the compressed power gain of the loop amplifier; F = the noise factor of the loop amplifier; k = the Boltzmann’s constant; T = the temperature (in degrees K); P0 = the carrier power level (in W) at the output of the loop amplifier; f0 = the carrier frequency (in Hz); fm = the carrier offset frequency (in Hz); QL = (πF0tg) = the loaded Q of the resonator in the feedback loop; aR and aE = the flicker noise constants for the resonator and loop amplifier, respectively.
To calculate the loaded QL in Equations 1 and 5, it is necessary to consider the unloaded Q (Q0) and the loading effect of the active device circuits and tuning networks. There, the influence of Y21+ has to be considered. The inverse of Y21+ is responsible for the loading and reduction of the resonator Q-factor3:
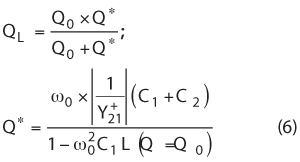
Based on the transformation of the loading of the device emitter’s differential impedance (resistance), it is possible to calculate the noise factor of the transistor under large-signal conditions.
The explicit expression for the phase noise £(ω) in dBc/Hz in terms of the known oscillator circuit parameters for the circuit shown in Figure 1 can be described by:3

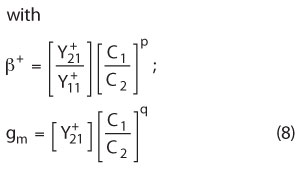
where Y21+, Y11+ is the large signal [Y] parameter of the active device, Kf is the flicker noise coefficient, AF is the flicker noise exponent, RL is the equivalent loss resistance of the tuned resonator circuit, Ic is the RF collector current, Ib is the RF base current, Vcc is the RF collector voltage, C1, C2 are the feedback capacitors, gm is the transconductance, Qu and QL are unloaded and loaded Q factors, and p and q (p = 1.3 to 1.6; q = 1 to 1.1) are the drive level dependent constant across base-emitter of the device.
Given an ideal resonator with no long-term drift, aging, or variation due to temperature, the tuning circuit would not be needed for a fixed frequency reference oscillator to correct the frequency drift, but in reality this is not the case. For practical applications, the resonator requires corrective measures to keep the frequency stable. In tunable crystal oscillator circuits, this is achieved through the use of tuning diodes with capacitance values that change as a function of applied voltage.
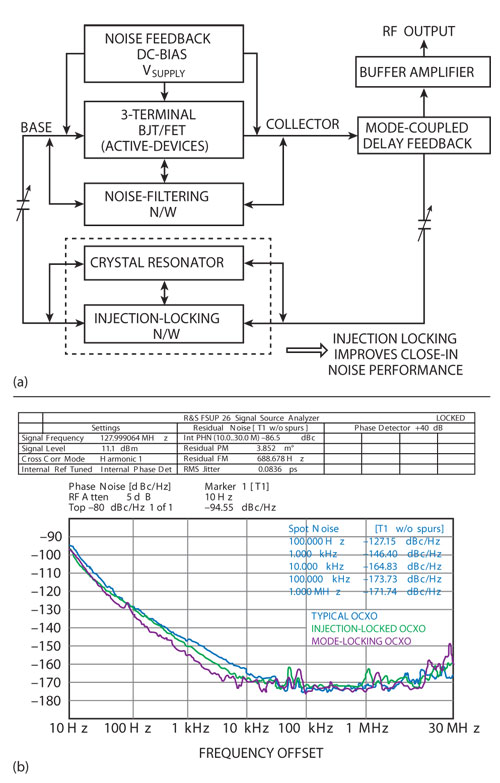
Figure 3 Typical block diagram (a) of a mode-coupled injection-locked 128 MHz crystal oscillator circuit (crystal Q = 80,000) and its measured phase noise (b).
High stability, low phase noise signal sources typically use quartz crystals as the resonator in the Colpitts and alternatively a Meissner type oscillator arrangement. Since the Colpitts oscillator uses a capacitive voltage divider, the crystal has to act as a high Q inductor; this means it is slightly detuned from its series resonant condition. Crystals have a Q from 50,000 (poor quality factor) to several million. Since they are mechanical resonators that are driven by the piezoelectric effect, they have fundamental, 3rd, 5th, 7th, and even 11th over tone modes. Unfortunately, due to undesired mode jumping, even in well-planned circuit design, it can become quite tricky to obtain the appropriate mode without jumping to other modes, which requires that special circuitry be added to the VCXO circuits. For example, if the fifth overtone mode is desired, a poorly designed oscillator may jump to the third overtone mode unexpectedly. One simple technique is to minimize the mode-separation by mode-locking techniques for preventing the mode-jumping and improving the stability of the crystal oscillator circuits. Figures 3a and 3b show the typical block diagram and phase noise plots of mode-coupled injection-locked 128 MHz OCXO, which may not be the best performance, but reasonably good for low cost OCXO and VCXO solutions and offer low-cost stable signal source solutions, applicable to both low and high Q-factor crystal resonator. While crystal oscillators have been used for many years, most oscillation optimization was done empirically rather than analytically. The demand for very high performance crystal oscillators with the ability to compensate for aging as a result of high drive levels, which are required for the improved phase noise, has triggered a new look at the possibility of applying new oscillator optimization techniques.
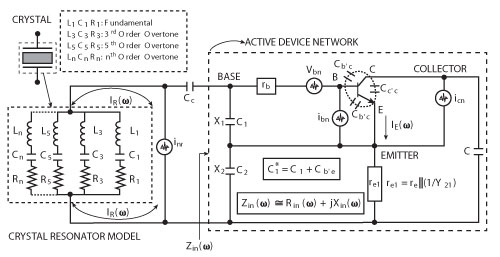
Figure 4 Typical crystal oscillator including noise contributions and odd order overtone modes.
Crystal Oscillator Design Examples
For high stability crystal oscillator operation, a method is needed to select a particular resonance mode, so that undesired modes are suppressed. One simple technique is to maximize the negative resistance generated from the active device network for a given particular mode and maximize the positive value of resistance for the unwanted modes. Figures 4 and 5 show typical overtone mode crystal oscillator circuit, illustrating the active device noise contributions and mode-coupling dynamics.
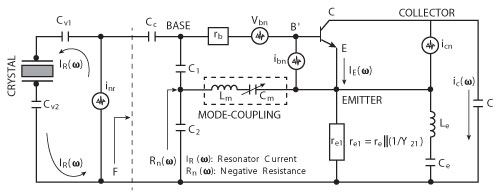
Figure 5 Typical crystal oscillator including mode coupling network for preventing mode-jumping.
To understand the design criteria for overtone mode selection, the input impedance of the transistor can be considered. From Figure 4, the input impedance Zin(ω) can be described by
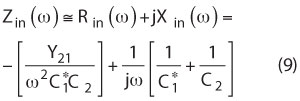
where C*1 = C1 + Cb'e
From Equation 9, the negative resistance and resonator drive level at the steady-state for the circuit shown in Figure 4 is given by:
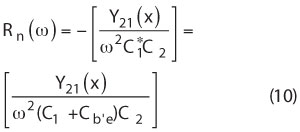
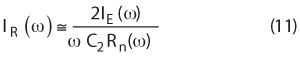
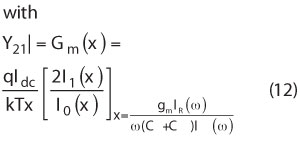
where I1(x) and I2(x) are modified Bessel functions of order 0 and 1, respectively. From Equations 10 and 11, the resonator current drive level IR(ω) can be lowered by increasing the value of feedback capacitor C2 for a given current IE(ω), but at the cost of reduction in the value of negative resistance Rn(ω), which is very much necessary for compensating the loss resistance associated with the desired higher overtone modes of the crystal resonator for realization of high frequency stable oscillation condition. Lower value of negative resistance Rn(ω) will require very high Q-factor crystal resonator, therefore it is not a cost-effective solution.
In order to maintain the same value of negative resistance Rn(ω) needed to compensate the loss resistance of the crystal resonator at steady-state oscillation, the value of the feedback capacitor C1 has to be reduced. There is a practical limitation of the minimum value of the C1, to be decided by a specified value of the load capacitance of the crystal resonator, which includes the intrinsic base-emitter capacitor (Cb'e) of the transistor. Moreover, drive-level parameters determine the overall nonlinearity, which causes amplitude-frequency effect and degrades the 1/f noise performances.
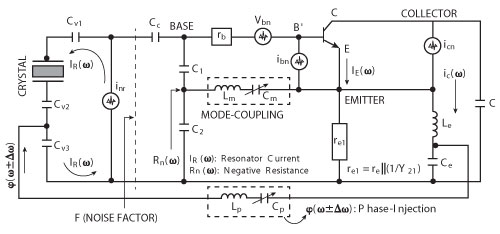
Figure 6 Typical mode-coupled phase-injected φ(ω±Δω) crystal oscillator, including noise contributions (transistor and resonator).
To demonstrate the new approach, a typical Colpitts configuration of crystal oscillator circuit was used as an example to apply the concept of phase-injection and mode-locking. This optimization can be accomplished by using mode-coupling (tuning the Lm-Cm at higher order modes) and a phase-injection φ(ω±Δω) mechanism for a given mode-coupling and drive-level IR(ω) (see Figure 6). The capacitor CV1 provides sufficient coupling for the oscillation growth (without CV2 and CV3), but at the cost of slow start-up characteristics and high drive level IR(ω). As shown in the figure, higher order modes are coupled through the output path and feedback to the point where frequency-drive sensitivity of the crystal resonator shows maximum group delay and faster slew rate, resulting in improved stability with reduced drive-level IR(ω).
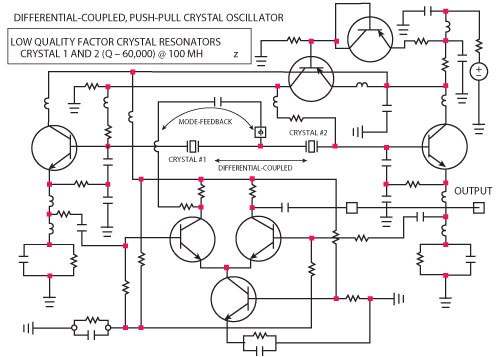
Figure 7 Schematic of a 100 MHz differential-coupled, push-pull, crystal oscillator circuit using inexpensive crystal resonators (Q ≡ 60,000).
For a low-cost, low-phase-noise crystal oscillator, self-injection-locking can be realized by a delay network in conjunction with the phase-injection network. A self-injection-locked oscillator has the ability to adjust its frequency to follow the locking signal, resulting in a comparatively higher locking range as compared to an external reference for a given figure of merit. The typical locking range of the self-injection-locked crystal oscillator can be described in terms of maximum change in frequency for given operating conditions as
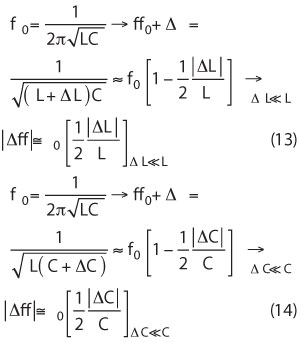
where ΔL and ΔC are the maximum change of the effective inductance and capacitance of the resonator tank circuit due to the injection-locking signal (realized by using a delay-line phase shifter and Δf is the maximum frequency shift that governs the locking range of the crystal oscillator). From Equations 13 and 14, the locking range is proportional to the maximum amount of the change of the inductance (ΔL) or capacitance (ΔC) caused by the injected signal through the delay line for achieving phase synchronization. For a given oscillator circuit topology and operating DC bias condition, it is important to note that the ratio of inductance to capacitance (L/C) of the resonator tank influences the drive-level and time-jitter fluctuations characteristics. The trick is to dynamically suppress the intrinsic random fluctuation and mode-jumping dynamics by optimizing the mode-coupling network in conjunction with phase-injection techniques. Figure 7 shows the simplified schematic for an enhanced-performance 100 MHz crystal oscillator circuit by incorporating techniques described in Equations 1 to 14. Figure 8 shows the simulated phase noise plots of crystal oscillator circuits using different topologies for a comparative analysis. Figure 9 shows the measured phase noise plots for an enhanced-performance 100 MHz crystal oscillator circuit.
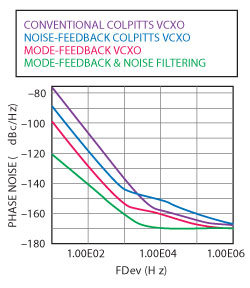
Figure 8 CAD simulated phase noise plots for 100 MHz crystal oscillators using different modes.
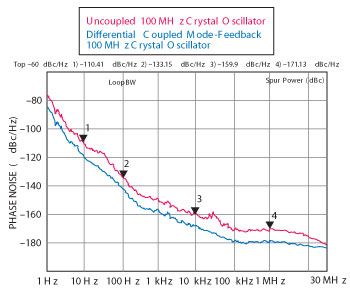
Figure 9 Measured phase noise plots for an enhanced-performance 100 MHz crystal oscillator circuit.
Figures 10 and 11 show the schematic and phase noise plots of a 5th overtone mode 100 MHz VCXO circuit to demonstrate the noise minimization techniques as described in Equations 1 to 14. For overtone modes, the equivalent circuit of crystal in the overtone branch can be computed by scaling the values of R, L and C in the fundamental resonant branch. If ‘f1’ is the fundamental frequency then the nth overtone frequency should be computed as
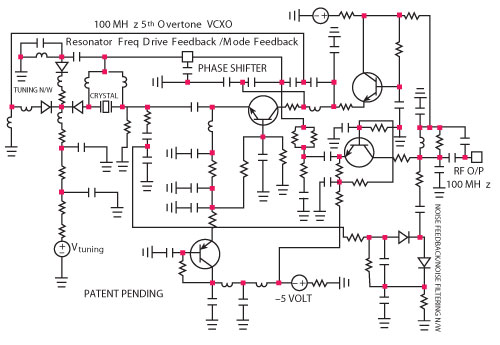
Figure 10 Typical schematic of 5th overtone mode 100 MHz VCXO circuit.
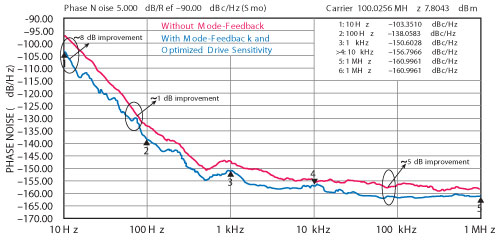
Figure 11 Measured phase noise of the 5th overtone mode 100 MHz VCXO circuits.
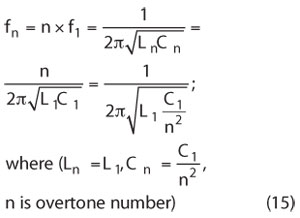
Wide pull VCXOs typically utilize fundamental crystals with large motional capacitance C1. Overtone operation is precluded if wide tuning range is desired. Also the resistor for the overtone branch gets scaled as Rn = R1n2, which implies that the negative resistance required to get oscillations on overtone is much larger than the value for fundamental mode. The fundamental frequency (lowest-mode) response is the most active due to a lowest value of Rn. If a large negative resistance is provided for the fundamental resonance, it could result in exciting an overtone mode also. For designing high frequency crystal oscillators, generally the crystal is excited on its overtone mode and care should be taken to suppress the unwanted fundamental resonance in such cases.
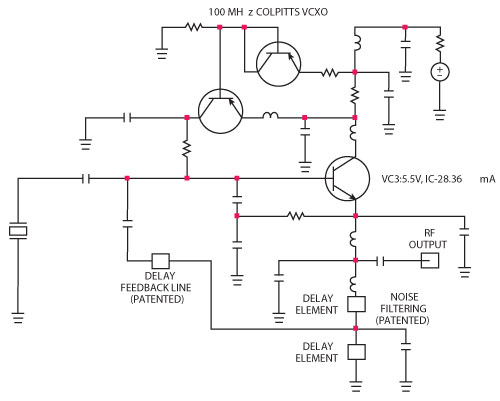
Figure 12 Typical schematic of a low phase noise, stable 100 MHz crystal oscillator using a mode-coupling mechanism.
Figure 12 shows the typical schematic of the mode-coupled 100 MHz crystal oscillator circuits by incorporating delay line noise filtering techniques. This approach is being applied to the development of high-performance VCXOs and can be extended to higher frequencies by incorporating phase-injection stubs across the crystal resonator at the desired operating frequency.
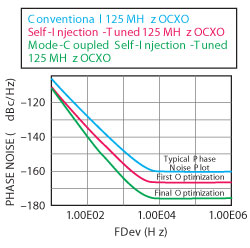
Figure 13 Typical CAD-simulated phase-noise plot of the 125 MHz OCXO circuit.
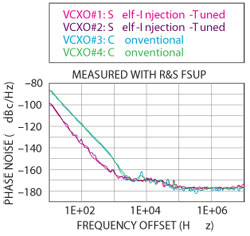
Figure 14 Measured phase-noise plots of the 125 MHz OCXO circuits.
Described is an approach to overcome the uncertainty associated with crystal resonator modeling and suggest the unified topology using differential-phase-shift-injection-locking (DPSIL) methods in conjunction with mode-coupled-delay-feedback (MCDF) technique that enables low cost low phase noise solutions for both fundamental and overtone-modes crystal oscillator circuits. DPSIL improves the close-in phase noise performance, whereas MCDF prevents mode-jumping and improves the stability and far out phase noise performance. Figure 13 compares the simulated 125 MHz OCXO with a first-pass optimization and with the best results from these new techniques. The CAD simulated results were validated with theory and measurements (see Figure 14). As shown, the phase noise plots of the 125 MHz OCXO circuit using the following topologies: without optimization (conventional topology), first optimization (self-injection-tuned topology) and final optimization (mode-locking-injection-tuned using delay line) are illustrated for comparative insights about the phase noise performance.
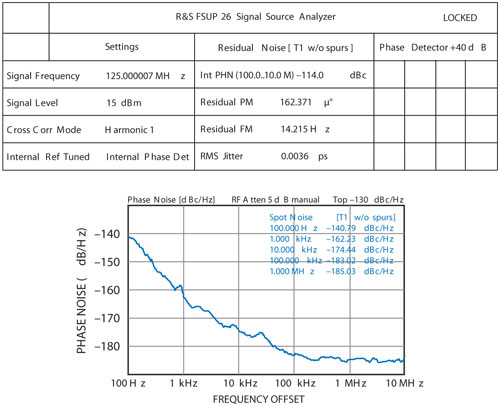
Figure 15 Measured phase noise plot of the 125 MHz DPSIL-MCDF OCXO circuit.
Figure 15 shows the measured phase noise plots for a 125 MHz OCXO circuit using DPSIL topology for the validation of the examples shown. The adaptive filtering techniques described, in conjunction with DPSIL-MCDF, suppress the intrinsic 1/f noise of crystal resonator, thereby improved close-in phase noise performance of 125 MHz OCXO circuits.
To the author’s knowledge, the reported phase noise performance of 125 MHz OCXO is the best performance to date, using crystal of unloaded Q = 80,000 for a given class and figure of merit. (See Table 1 online at www.mwjournal.com/OCXOresults for a summary of the measurements.)
References
- D.B. Leeson, “A Simple Model of Feedback Oscillator Noise Spectrum,” Proceedings of the IEEE, Vol. 54, No. 2, February 1966, pp. 329-330.
- U.L. Rohde and T.T.N. Bucher, Communication Receivers Principles & Design, McGraw Hill, New York, NY, 1988, p. 302.
- U.L. Rohde, A.K. Poddar and G. Boeck, The Design of Modern Microwave Oscillators for Wireless Applications: Theory and Optimization, John Wiley & Sons, New York, NY, 2005.
- Y. Tsuzuki, T. Adachi and J.W. Zhang, “Fast Start-up Crystal Oscillator Circuits,” 1995 IEEE International Frequency Control Symposium Digest, pp. 565-568.
- X. Huang, Y. Wang and W. Fu, “The Design and Implementation of a 120-MHz Pierce Low-phase-noise Crystal Oscillator,” IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, Vol. 58, No. 7, July 2011, pp. 1302-1306.
- K. Sakamoto, K. Kubo and K. Ono, “Development of Ultra Low Noise VHF OCXO with Excellent Temperature Stability,” Proceedings of the 2008 IEEE International Frequency Control Symposium, pp. 1246-1250.
- J. Everard and K. Ng, “Ultra-Low Phase Noise Crystal Oscillators,” Proceedings of the 2007 IEEE International Frequency Control Symposium, pp. 1246-1250.
- A.K. Poddar and U.L. Rohde, Crystal Oscillators Design, Wiley Encyclopedia of Electrical and Electronics Engineering, pp. 1-47.
