In a radar system, the use of pulse modulation or “compression” provides enhanced spatial resolution as well as an extended range for a given output power level. Consequently, this technique is widely used in current- and next-generation radar systems. A simple block diagram of a compressed pulse radar system is shown in Figure 1.

Fig. 1 Simple block diagram of a pulse compression radar system.
An expanded Linear Frequency Modulated (LFM) chirp pulse is one option for the transmitted pulse. The received pulse is down converted and processed by the matched or correlation filter, whose frequency response is a complex conjugate of the coded filter. The compression filter readjusts the relative phases of the frequency components with the appropriate delay so that a narrow compressed pulse is reproduced. This compressed pulse is also accompanied by sin(x)/x time sidelobes responses. Amplitude weighting functions are applied to the rising and trailing edges of the pulse to reduce the time sidelobe levels. If there are two closely spaced overlapping echoes, then they will be separated into distinct output pulses due to the processing of their modulation—so long as they are separated by a range the equivalent of half the compressed pulse (a round trip equal to the full compressed pulse).
Unfortunately, traditional RF pulse measurements become less effective predictors of performance in radars that use pulse compression. For example, the width of an uncompressed radar pulse is directly related to spatial resolution. In contrast, the resolution depends on pulse width, chirp bandwidth and chirp linearity in a compressed radar system that uses LFM chirp pulses. Within the field of radar development, a technique called the time Sidelobe Level (SLL) measurement has emerged as a viable solution. This method distills a wide range of potential signal impairments down to a simple metric that can be used to determine if radar performance will fit the intended application.
SLL is normally measured by illuminating a reference target and making the measurement at the radar receiver’s pulse compression filter output. To make transmitter-only measurements, a Vector Signal Analyzer (VSA) can be used as an ideal radar pulse compression receiver. This is similar to Error Vector Magnitude (EVM) measurements commonly used with communication signals, where the VSA acts as an ideal demodulator and takes mathematically generated ideal waveforms, which are compared to the measured waveform.
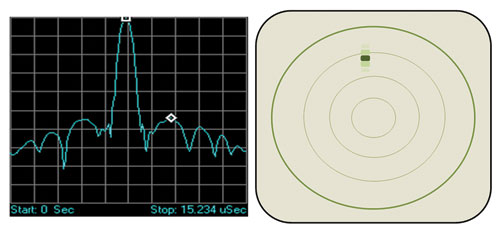
Fig. 2 Time domain representation of a chirp pulse after compression and how it might look on a PPI radar display.
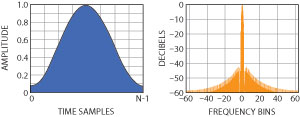
Fig. 3 Time and frequency domain graphs of the hamming windowing function.
Sometimes referred to as range sidelobes, time sidelobes are a result of using pulse compression techniques. They are produced when the ideal radar return is convolved with the response of the less than ideal correlation filter, during the compression process or when a non-ideal radar return (from a non-ideal transmitted pulse) is convolved with the response of the less than ideal correlation filter or some combination of the two. This causes some of the energy in the return pulse to lie outside the pulse bandwidth. In the time domain, this is indicated by a spreading in range (time) of the return pulse, particularly in the presence of ground clutter or transmit signal anomalies caused by imperfections in the transmitter path (see Figure 2).
Windowing or amplitude weighting of the output signals is generally used to reduce the time sidelobes to an acceptable level. Simply measuring a signal for a finite time is equivalent to multiplying the signal by a uniform function or window of unit amplitude. Windowing involves multiplying the signal data by a function that smoothly approaches zero at both ends. The theoretical sidelobe level for a rectangular window (or no window) is –13.2 dB, whereas for the Hamming window, the theoretical level is –42.8 dB. In Figure 3, the time and frequency domain representations of the Hamming windowing function are shown. Windowing can be applied in either domain. As a side effect, signal weighting will result in the loss of signal-to-noise ratio. Some of the more commonly used windowing functions are shown in Table 1 with their suppression levels and signal-to-noise losses.

Making the Time SideLobe Measurement
The Agilent 89600 VSA software or MATLAB from Mathworks can perform a correlation filter function that correlates or compares the transmitter output signal to an ideal waveform. The ideal waveform can be built using MATLAB. It requires knowledge of the important parameters of the signal to be measured, such as FM bandwidth, pulse width and sample rate of the VSA during the measurement (VSA sample rate equals 1/ [1.28*VSA span]). The compressed pulse is a much narrower pulse compared to the transmitted pulse. The pulse compression ratio is a function of the time bandwidth product of the chirp and the window used for the correlation filter. The SLL represents the ability of the transmitter and receiver to separate small, close-by target return echoes from large ones.
The pulse waveform is created in MATLAB and then downloaded to the arbitrary waveform generator (AWG). The mathematically generated ideal pulse is also then available in a digital form for use when making just a single measurement, such as when characterizing the transmitter only for SLL. Alternatively, the ideal pulse could be measured at different points at the front end of the receiver to characterize filter performance. This would be done using two channels on an oscilloscope. Either an oscilloscope or signal analyzer can be used to correct the IQ waveform played from the AWG for phase and amplitude flatness across the bandwidth (BW) of the signal.
The next step is to look at the side- lobe level. For this, the VSA’s Math Functions or MATLAB incorporated into a User Defined Function on the oscilloscope will be used to perform a cross correlation between the measured pulse and the ideal pulse. This simulates the radar receiver correlator or compression filter. To simplify the calculation, the math identity of time correlation equals frequency domain multiplication will be used. Hamming windows are applied to both the measured and ideal waveform during the translation. For reference, the auto correlation of the ideal chirp is computed as well. This represents the best width and sidelobes that could be attained.
The measured frequency data (real and imaginary) is multiplied by the ideal pulse. This result is processed with the inverse fast Fourier transform (IFFT) function to produce the time cross correlation needed for the SLL measurement.
Measured(t) × 3 Ideal(t) = IFFT
[Measured(f) * conj[Ideal(f)]]
Where:
Measured(f) = window * FFT (Measured(t))
Ideal(f) = window * FFT (Ideal(t))
The measurement results are shown in Figure 4.
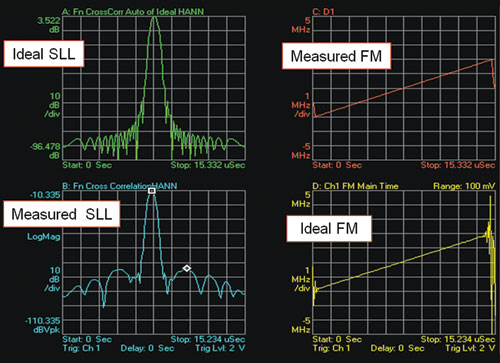
Figure 4 SLL measurement results.
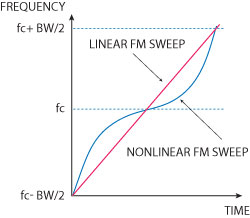
Fig. 5 Frequency sweep across the width of a nonlinear FM chirp pulse.
A nonlinear FM waveform (see Figure 5) provides advantages over the LFM one. The nonlinear FM waveform requires no weighting for time-sidelobe suppression since the FM modulation of the waveform is developed to provide the desired time and spectrum response. The nonlinear characteristics are chosen to accommodate FFT artifacts and imperfections in the system hardware or waveforms. The drawback of nonlinear FM systems is that they are complex and costly to implement.
Other types of pulse compression radars use pulses coded with a stream of bits. The bit pattern is chosen such that it has a high correlation peak and the receiver again performs a compression filter by cross correlating against the ideal transmitter waveform. The performance metrics used with these waveforms include EVM, modulation accuracy and SLL.
The waveform coding uses BPSK or QPSK modulation and can be treated as a short burst of digital communications-like signal. The flexible demodulator within the Agilent VSA software can be used to extract the EVM quality metric. In addition, numerous error and troubleshooting features can be exploited.
One useful modulation coding is the Barker, Frank and polyphase code trains. Barker codes are the binary phase codes with the property that the peak sidelobes of their autocorrelation functions are all less than or equal to 1/N in magnitude, where N is the code length and the correlator output peak is normalized to 1.0. The more bits within a code train, the lower the time sidelobe level. The VSA software’s digital demodulator can be applied for simplifying the testing of the 13 bit Barker coded burst by considering it a short vector modulated signal of symbol rate of 13/(pulse width). The theoretical SLL value of a 13 bit Barker coded pulse is –22.3 dB. Figure 6 shows the measurement and calculation results.
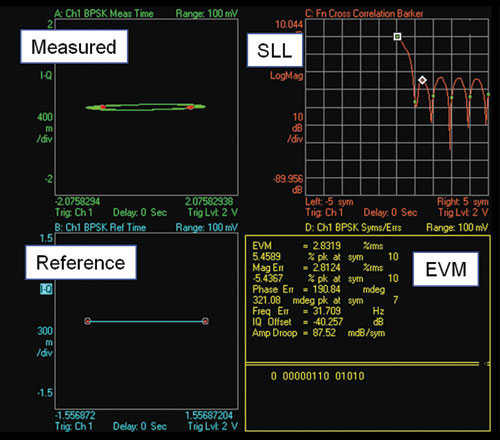
Figure 6 SLL and EVM of a 13 bit Barker coded pulse.
Spatial resolution is often an essential part of the system acceptance criteria. Because the time from the main correlation lobe to the minimum discernable sidelobe is directly related to the minimum spatial resolution, SLL offers an effective go/no-go assessment of a radar system’s field performance. SLL also provides assurance that no other internally generated sidelobe will affect the overall threshold performance of the radar. The correlation function is also directly tied to the probability of target detection. From this, a sufficiently low SLL value ensures the radar hardware under test will have a dynamic range wide enough to detect weak target signals.
At the component level, time sidelobe testing can help identify problems with analog microwave components. The typical approach is to patiently work through the process of measuring parametric characteristics and then sifting through the results and identifying potential problems. Instead, time sidelobe levels can be evaluated for impairments at any point within a system—and this makes it possible to rapidly assess if the radar pulses can deliver the desired level of performance.
This ability to assess pulse quality virtually anywhere within a radar system—from transmitter to receiver detector—makes SLL a valuable diagnostic tool. For example, one quick SLL measurement at the transmitter output can instantly pinpoint either the transmitter or receiver as the source of problems. Subsequent measurements can quickly isolate signal impairments that are preventing radar performance from meeting system requirements.
Time sidelobe measurements are easy to perform with popular Agilent signal analyzers, oscilloscopes and logic analyzers equipped with Agilent 89600 VSA software. Preparation for the measurement requires creation of the ideal pulse waveform, importation of the ideal pulse into the VSA software and some trace math. Once the setup is complete, time sidelobe measurements are easy to perform and can be used to gauge key performance traits, isolate signal impairments, diagnose system problems and find problems at the component level.
