With the rapid development of modern communications, efficient utilization of more and more frequency channels is necessary. Microwave filters have been widely used in modern communication systems. In recent years, more novel filters, using new technologies, continue to challenge traditional radio frequency (RF) components with ever more stringent requirements, including better properties, smaller dimensions and lower power consumption.1
Periodic structures have recently attracted much attention in the microwave and millimeter-wave community, owing to their filtering properties or inhibition of signal propagation in certain directions. These structures have been usually referred to as electromagnetic bandgaps (EBG) or electromagnetic crystals. EBG structures can be embedded in the dielectric substrate or etched in the metal layer.2 This helps to suppress the surface waves and results in a better radiation pattern, higher transmission efficiency and good slow-wave3 characteristic to obtain frequency-selective features.4 EBG structures realized on metal layers are useful for constructing filters, including bandstop filters (BSF),5 lowpass filter (LPF)6 and bandpass filter (BPF),7 phase shifters,8 power dividers,9 antennas10 and resonators.4 In these studies, the RF components with EBG slot or CPW-fed slot structures are designed to improve radiation patterns and to reduce the higher order harmonics, obtaining good ratio characteristics.
EBG structures can be patterned on metal layers, such as the ground plane or the signal line of microstrips,7 as well as coplanar waveguide (CPW) transmission lines.3 The EBG lattice can offer extreme flexibility in the design of filters based on CPW transmission lines. The inductance and capacitance values of the EBG can be adjusted by varying the dimensions of the EBG lattice geometries, thus can effectively cancel the reactive part of the characteristic impedance.
In this article, a broadband bandstop filter, with sharp cut-off frequencies, is constructed by cascading two dual-ear EBG cell resonators with good performance and compact-size CPW transmission lines. The circuit models of the EBG structures are derived by an equivalent circuit approach and full-wave electromagnetic simulation is used for extracting the values of the lumped elements in the circuit. The 20 dB bandwidth of the BSF is 2 GHz (9.9 to 11.9 GHz) and the center frequency is 11.5 GHz. The 20 dB fractional bandwidth is 18.3 percent. In the 20 dB stopband range, the return loss ripple is less than 0.5 dB. The proposed BSF is fabricated using surface micromachining, and measurement and simulation results are in agreement.

Figure 1 EBG unit (a) etched lattice shaped (ELS) unit and (b) the dual-ear unit.
The EBG Unit Cell
An etched lattice shaped (ELS) EBG unit is machined on a CPW line with a 50 Ω characteristic impedance (G/W/G= 60/100/60) for good impedance matching, as shown in Figure 1. The substrate is high resistivity silicon ( = 4000 Ω cm) with a dielectric permittivity of εr = 11.9 and a thickness of 450 μm. The metal thickness of CPW signal line is 0.5 μm, and the other parameters are h = 800 μm, a = 350 μm, b = 300 μm, d = 60 μm and s = 700 μm. The width of the ground line is sufficiently larger than that of the signal line, and is assumed to be semi-infinite (set as 2000 μm in the simulation). The RF performance of the structure is shown in Figure 2. The 3 dB bandwidth is 9.5 GHz, from 18.4 to 27.9 GHz. The 20 dB bandwidth is 1.7 GHz, from 23.3 to 25 GHz.

Figure 2 Comparison of EM and circuit simulation RF performance of EBG units (a) ELS unit and (b) EBG-DE structure.

Figure 3 Equivalent parallel circuit model of the EBG cell.
From the simulation results, the lumped-element equivalent circuit is derived by cascading two parallel resonant circuits to model this EBG unit cell, as shown in Figure 3. Each EBG unit cell is represented by two series RLC tanks instead of only one as that of Karim.11 It is necessary to extract the lumped circuit parameters to analyze the EBG unit deeply. The equivalent impedance equation of the single resonant model may be expressed as

Where the subscripts "1" and "2" denote the two different resonant circuit parameters. According to microwave network theory, assuming that R>>Z0, the S-parameters are reduced to

From Elamaran et al.,8 the equivalent circuit parameters, C1 and C2 can be extracted as

Then, the parameters L1 and L2 can be extracted from 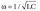 . The resistances R1 and R2 of the circuit can be obtained approximately from the resonant frequencies, ω1 and ω2, respectively.
. The resistances R1 and R2 of the circuit can be obtained approximately from the resonant frequencies, ω1 and ω2, respectively.

Therefore, this model can predict the EBG unit cell over the relatively wide frequency range from DC to 40 GHz, in which the circuit simulation results and the EM simulation results show good agreement. The resistors, capacitances and inductances are evaluated from the resonant frequencies of the EBG unit cell and listed in Table 1.

The Bandstop Filter
EBG Dual-Ear (DE) Structure
From the above analysis, it is implied that it is difficult to change the resonant frequency over a large range, unless the dimensions of the ELS-EBG unit cell have a large change, and the cut-off frequencies of the filter using the ELS-EBG units are not sharp enough to be used in this application. Moreover, the cut-off frequency of the filter, using dual-ear structures, can be adjusted and become sharper than before.12 For these considerations, an improved compact EBG structure with dual-ear structures (EBG-DE) based on the ELS-EBG unit is introduced (see Figure 1). The dimensions of the EBG-DE structure, m, n, o, p, q, r, u, and v, are 300, 40, 120.6, 559, 108, 50, 220 and 42.66 mm, respectively.
The unit cell's equivalent circuit is represented by two series RLC tanks analyzed like before, and the EBG-DE structure simulation curves are shown in Figure 2. It is easy to observe that the EM simulation curves are consistent with the circuit simulation curves, which means that the two series RLC tanks circuit model is fit for the EBG-DE structure as well. The circuit model's parameters, including resistances, capacitances and inductances, are shown in Table 1.

Figure 4 Frequency response comparison between ELS-EBG and EBG-DE structure.
Frequency Response Compared Between ELS-EBG and EBG-DE
The comparison of the frequency responses between ELS-EBG and EBG-DE is shown in Figure 4. Compared with the ELS-EBG structure, the first resonant frequency of the improved EBG-DE structure is shifted from 24.2 to 11.1 GHz. The shift of the resonant frequency with a large range of 13.1 GHz is realized using the dual-ears structure.
The distributed capacity and inductance of the EBG-DE structure are increased by the introduction of dual-ears structures, listed in Table 1. Therefore, the resonant frequency of the improved EBG-DE structure is decreased, as shown in the figure. At the same time, the resistance of the BSF using the EBG-DE structure is increased, and results in the increase of the insertion loss.
The EBG-DE unit cell can be used in an oscillator at 11.1 GHz. For the oscillator, the frequency spectra of phase perturbation δΦ(ω) of the oscillating signal is derived using the phase noise estimation:13

where

In this oscillator model, the active device for negative resistance generation is represented by Zd = Rd + jXd and the impedance of the resonator is represented by Zc (ω)= Rc + jXc. The entire circuit is expressed as a series connection of Zd and Zc (ω), where e(t) represents noise that may be present.
From Equation 6, the reduction of phase noise can be achieved by increasing the magnitude of Zc'(ω0), which means a drastic impedance variation of a resonator with respect to frequency at the point of resonance.
From Table 1, the equivalent resistances extracted from the equivalent circuit of the ELS-EBG unit cell are 1.6465 and 1.6083 kΩ, which are much less than the equivalent resistances of the DE-EBG unit cell, 11.109 and 9.9282 kΩ. This means that the magnitude of Zc(ω0) of the oscillator using the EBG-DE unit cell is larger than that using the ELS-EBG unit cell. Thus, the oscillator using the EBG-DE unit cell has sharper frequency characteristics than that using the ELS-EBG unit cell.
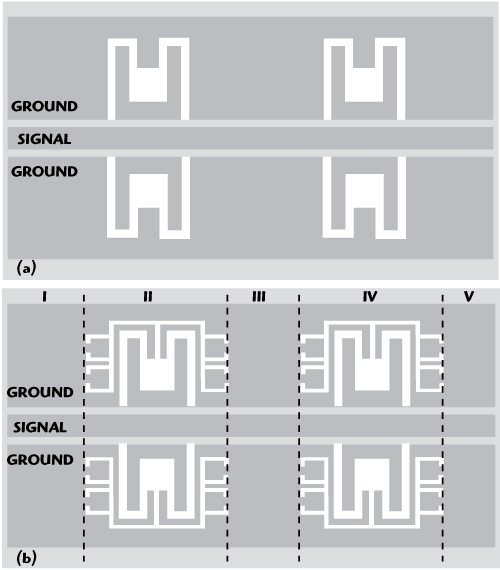
Figure 5 Bandstop filters made by cascading two proposed EBG structures (a) ELS-EBG structures and (b) EBG-DE structures.

Figure 6 Simulated performance of two cascaded EBG structures (a) ELS-EBG and (b) EBG-DE.
BSFs Constructed by Cascading EBG-DE and ELS-EBG Structures
According to the preceding analysis, bandstop filters with wider bandwidth are constructed by cascading two proposed EBG units, including the ELS-EBG and EBG-DE structures, as shown in Figure 5. The length of the filter is approximately 4000 μm.
The RF performance of the filters is shown in Figure 6. The stopband of the filter using EBG-DE units lies within X-Band, while the stopband of the filter using ELS-EBG units stays within K-Band.
The 3 dB bandwidth of the BSF using the ELS-EBG structure is 10.1 GHz, from 17.9 to 28 GHz and the center frequency is 24.3 GHz. The 20 dB bandwidth is 4.6 GHz, from 21.2 to 25.8 GHz. In the 20 dB stopband range, the return loss ripple is less than 0.19 dB. The 3 dB bandwidth of the BSF using the improved EBG-DE structure is 4.2 GHz, from 8.6 to 12.8 GHz and the center frequency is 11 GHz. The 20 dB bandwidth is 2 GHz, from 9.9 to 11.9 GHz. In the 20 dB stopband range, the return loss ripple is less than 0.05 dB. It is easy to see that the BSF using the improved EBG-DE structure has a narrower stop-band width and a smaller ripple than the BSF using ELS-EBG structure.

Figure 7 Frequency response comparison between filters using ELS-EBG and EBG-DE structures.
The comparison of the frequency responses between the filters using ELS-EBG and EBG-DE structures is shown in Figure 7. Comparing the two filters, the cut-off frequencies of the filter using the EBG-DE unit cell is sharper. From the simulation results, the sharp selectivity is observed and it is noticed that the 20 dB stopband is from 10.3 to 12.6 GHz. The stopband return loss is less than 0.5 dB. In the passband, the insertion loss is less than 0.6 dB, and the return loss is greater than 8 dB. The 3 dB fractional bandwidth is 34.6 percent. Thus, the filter with EBG-DE structure possesses a better frequency selectively and it would be possible to design sharply selective bandstop filters with the dual-ear EBG structure.

Figure 8 Equivalent parallel circuit model of the BSF composed of two cascaded proposed EBG-DE structures.
Equivalent Circuit Analysis
The equivalent circuit of the BSF, formed by cascading EBG-DE structures, is shown in Figure 8. The conformal mapping and Green's function methods are used to calculate the per unit length capacitance for a finite electrode thickness with the buffer layer,14 which can be written as

Where C0 is the per unit length capacitance of the CPW without considering the thickness of the metal layer, Ct is the capacitance value increasing caused by side-face area after considering the thickness of the metal electrodes. Approximate expressions containing empirical fitting parameters are given below:15

where 
a1= 0.49254, a2 = 0.01709, a3= 0.21918, and a4 = 0.10357. Here K is the complete elliptic integral of the first kind, ε0 is the permittivity of free space and εr is the relative permittivity of the material.
In Figure 5, the layout of the BSF is divided into five parts, two EBGs and three CPWs. According to microwave theory,15 a CPW transmission line can be modeled as a lumped element with a very large number of elements. The total line length has been divided into an infinite number of sections.
Each lumped element represents an infinitesimal piece of the physical transmission line. The values of ΔR, ΔC, ΔL and ΔG are the resistance per length, capacitance per length, inductance per length, and conductance per length, respectively. These are the distributed parameters of the transmission line.
From the equations above, it is easy to obtain values of capacitances in the equivalent circuit:

In Figure 5, the length of part I and part V is l1, and the length of part III is l2. However, the CPW parts are short enough and it is reasonable to neglect their resistances and conductances. According to microwave theory, Lg can be written as

Where ω represents the resonance frequency of the CPW at part I and also at the others. Additionally, the equivalent circuit of the BSF composed by cascading two EBG-DE structures is shown in Figure 8. The parameters, including capacitances, Cp and Cg, and inductances, Lp and Lg, are listed in Table 1. The RF performance, compared between the EM and circuit simulation, is shown in Figure 9. The circuit simulation results agree well with the EM simulation results.

Figure 9 Comparison between EM and circuit simulation of two cascaded EBG-DE structures.

Figure 10 Photograph of an EBG dual-ear structure.
Measurement Results and Discussion
The designed BSF structures are fabricated on a high resistivity silicon substrate (ρ = 4000 Ω cm) using a surface micromachining fabrication technology. A 1000 Å thick thermal oxide was introduced on the substrate as buffer layer. The metal layer is made by sputtering a 0.5 μm thick aluminum layer, with careful stress control. The final BSF patterns are defined by lithography and wet etching. Compared to normal MMIC fabrication, the surface micromachining technology can precisely control small dimensions and mass production can be obtained. An optical photo of EBG dual-ear structure is shown in Figure 10.
The RF performance of the BSFs is obtained using an HP8510C vector network analyzer and a RF probe station with 150 μm probes. A full thru-reflect-line (TRL) routine is used to calibrate with the NIST software MULTICAL.
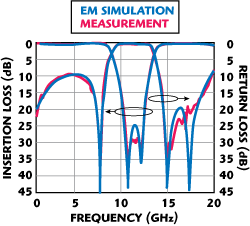
Figure 11 Comparison between simulated and measured performance of the EBG-DE bandstop filter.
Figure 11 shows the measured results for the BSF using EBG-DE units. The measurement results of the BSF made by cascading the proposed double EBG-DE units agree well with the simulated results. The small difference between the simulation results and the measurement results can be attributed to the fabrication error.
Conclusion
In this article, a bandstop filter using novel ELS-EBG structures has been studied. An equivalent circuit is provided to show the performance of the ELS-EBG structure with different dimensions. An improved EBG-DE structure with compact size has a low resonant frequency. A sharp bandstop filter with good performance is made by cascading two EBG-DE unit cells. The measurement and simulation results of the BSF agree well. It is expected that the EBG-DE structure for CPW will have potential applications in RF and microwave circuits.
Acknowledgment
This work was supported by the Fundamental Research Funds for the Central Universities (BUPT No. 2009RC0302).
References
- J.S. Hong, M.J. Lancaster, "Microstrip Filters for RF-Microwave Applications," John Wiley & Sons, New York, NY, 2001.
- M.F. Karim, A.Q. Liu, A. Alphones, X.J. Zhang and A.B. Yu, "CPW Band-stop Filter Using Unloaded and Loaded EBG Structures," IEEE Proceedings on Microwave and Antennas and Propagation, Vol. 152, No. 6, December 2005, pp. 434-440.
- L. Zhu, "Effective 1-D Material Properties of Coplanar Waveguide Based EBG and Meta-materials," 2008 International Workshop on Metamaterials Digest, Nanjing, China.
- A. Özlem and A. Görür, "Slow-wave CPW Resonator with Defected Ground Structure (DGS) for Filter Applications," Microwave and Optical Technology Letters, Vol. 48, No. 2, 2006, pp. 229-233.
- X.J. Zhang, A.Q. Liu, A.B. Yu and Z.X. Shen, "MEMS-based Photonic Bandgap (PBG) Band-stop Filter," 2004 IEEE MTT-S International Microwave Symposium Digest, Vol. 3, pp. 1463-1466.
- D. Ahn, J. Park, C. Kim, J. Kim, J. Park, Y. Qian and T. Itoh, "A Design of the Low-pass Filter Using the Novel Microstrip Defected Ground Structure," IEEE Transactions on Microwave Theory and Techniques,Vol. 49, No. 1, January 2001, pp. 86-93.
- N.C. Karmakar and M.N. Mollah, "Investigations into Nonuniform Photonic Bandgap Microstripline Low-pass Filters," IEEE Transactions on Microwave Theory and Techniques, Vol. 51, No. 2, Part 1, February 2003, pp. 564–572.
- B. Elamaran, I.M. Chio, L.Y. Chen and J.C. Chiao, "A Beam-steerer Using Reconfigurable PBG Ground Plane," 2000 IEEE MTT-S International Microwave Symposium Digest, pp. 835-838.
- D. Packiaraj, A. Bhargavi, M. Ramesh and A.T. Kalghatgi, "Compact Power Divider Using Defected Ground Structure for Wireless Applications," 2008 IEEE International Conference on Signal Processing, Communications and Networking Digest, pp. 25-29.
- B.L. Ooi, "Novel Electromagnetic Bandgap-fed Tri-band Coplanar Slot Antenna," Microwave and Optical Technology Letters, Vol. 49, No. 4, April 2007, pp. 954-960.
- M.F. Karim, A.Q. Liu, A. Alphones, X.J. Zhang and A.B. Yu, "CPW Band-stop Filter Using Unloaded and Loaded EBG Structures," IEEE Proceedings on Microwave Antennas and Propagation, Vol. 152, No. 6, December 2005, pp. 434-440.
- J.S. Hong and M.J. Lancaster, "Couplings of Microstrip Square Open-loop Resonators for Cross-coupled Planar Microwave Filters," IEEE Transactions on Microwave Theory and Techniques, Vol. 44, No. 11, November 1996, pp. 2099-2109.
- K. Kurokawa, "Some Basic Characteristics of Broadband Negative Resistance Oscillator Circuits," Bell System Technical Journal, Vol. 48, No. 6, July-August 1969, pp. 1937–1955.
- H. Chung, W.S.C. Chang and E.L. Adler, "Modeling and Optimization of Traveling-wave LiNbO3 Interferometric Modulators," IEEE Journal of Quantum Electronics, Vol. 27, No. 3, March 1991, pp. 608-617.
- D.M. Pozar, "Microwave Engineering," 3rd Edition, John Wiley & Sons, New York, 2005.
