Metal-insulator-metal (MIM) capacitors, (MIM caps) have played a vital role in the design of a wide variety of MMIC circuits, particularly where low loss/high-Q is a critical design requirement. Because of their ease of fabrication, they can be found in the design kits of both silicon and compound semiconductor (GaAs as well as GaN) technologies. When used as matching elements in a critical RF signal path, such as in the output network of a power amplifier (PA), the resistance of the MIM has a direct impact upon the achievable gain and PAE. When used in filtering applications, the resistance of the MIM directly affects the achievable Q of the associated network. Consequently, the accurate determination of the series resistance of the MIM is a critical requirement for accurate circuit design. If the MIM is to be used in a shunt configuration (to RF ground), then the same requirement holds with respect to modeling of the associated substrate via or (through) substrate via (SVIA).1

Measurement Problems and Solutions
Determination of the series resistance of MIM capacitors via "standard" S-parameter measurement methods has been proven to be a long-standing problem, primarily due to: (1) the ultra-low impedances presented by the DUT, (2) the high degree of accuracy that is required in order to resolve the difference between the resistive and reactive components and (3) the inability to resolve the finite resistive contribution due to probe contact. Standard S-parameter measurement-based attempts at characterization of ultra-low resistance passives typically utilize test structure designs in which the DUT is placed in either the series or shunt configuration, as defined in Table 1.
The characteristics of the device are thus determined via analysis of S21 (transmission), or S11 (reflection) data, respectively. The accuracy associated with either type of measurement differs according to the ability of the VNA to resolve the real and imaginary components of low level test signals within the residual (post calibration) dynamic range. Depending upon the VNA architecture, the resulting "phase accuracy" is frequency dependent, and is typically maximized (for a given measurement type) at minimum IF bandwidth, under low power RF drive.
A finite resistance results when the RF probes come in contact with the launch lines of the test structure. The resistance is the result of the work function associated with the dissimilarity in metal systems. This contact resistance (typically on the order of 30 m-Ω < PCR < 60 m-Ω) cannot be removed through the process of calibration, and is always present whenever a one- or two-port measurement is made.2,3
Repeatability of probe placement introduces variability in terms of the PCR, which prevents the accurate determination of the statistical characteristics of the underlying series resistance. The problem of (RF) probe contact (and its associated variability) is resolved by using test devices designed in the "series-shunt" configuration, while taking advantage of a special condition of the transmission measurement which arises when measuring shunt resonant devices.

Figure 1 Series-shunt configured SVIA.
Test Structure Design
Layouts for "series-shunt" configured SVIA and MIM cap test structures, suitable for high frequency (> 50 GHz) on-wafer RF characterization, are shown in Figures 1 and 2. Both test structures incorporate fixed length launchers, which feature wideband CPW-to-microstrip transitions and probe indexing markers at both ports 1 and 2.

Figure 2 "Series-Shunt" configured MIM cap.
The SVIA test structure is designed such that the physical via is connected directly to the measurement reference plane at the point where the ends of the launch (transmission) lines interconnect. This design configuration was chosen in order to validate that de-embedding is not necessary. The MIM cap test structure incorporates capacitors, defined as square geometries in order to tie the estimation of resistance directly to measured process (PCM) specifications. In the case where MIM caps are defined using two-level metal processes (typical of GaAs and GaN technologies), the sheet resistances associated with the top and bottom plate metals are the only factors that need be considered. In silicon technologies, however, one needs to also consider how to reconcile the resistance associated with the use of multiple via "posts" in the interconnection of the top plate.4

Figure 3 "Series-Shunt" MIM cap detail.
The MIM cap test structure utilizes the identical launch at both ports. However, it is intentionally embedded within an additional 1 mm of (transmission) delay in order to test the validity of the Thru standard based de-embedding methodology. Each test structure is designed such that its size varies according to the "insertion length" of the DUT. In this manner, de-embedding with a common set of (embedding) transmission line characteristics is facilitated. A detail view of the MIM cap, highlighting the sources of residual measurement resistance is shown in Figure 3. The detail shows the use of a thick airbridge metal to connect the MIM cap to the transmission line, as well as to the top of the SVIA. An estimate of the resistances associated with all of the metal interconnects is provided in Table 2.
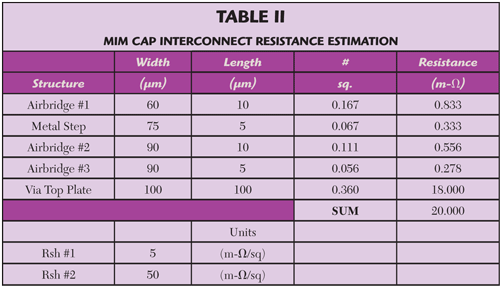

Figure 4 SVIA lumped element equivalent circuit.
Equivalent Circuits/Models
The equivalent circuit for the SVIA is defined using ideal lumped-element equivalent-circuit (LE-EC) elements as shown in Figure 4. Similarly, the equivalent circuit for the shunt-connected MIM cap is defined in terms of ideal LE-EC elements, as is shown in detail in Figure 5. For analysis purposes, a low frequency approximation simplification of the MIM Cap LE-EC is made by combining each of the components of the total series resistance in to a single element (Rs_total), as also shown.

Figure 5 (a) "Shunt-connected" MIM cap lumped element equivalent circuit and (b) simplified MIM cap.
Measurement Theory
As was described,2 the "S21-Shunt" measurement technique is the RF equivalent of the DC measurement procedure that is used to make highly precise resistance measurements. Because of the unique advantages offered by the technique, the derivation of the series impedance (Zseries) shown in Figure 6 is repeated here.

Figure 6 S21-shunt test configuration.
Using the 50 Ω test configuration shown schematically in the figure, the series impedance (Zseries) is derived in terms of the simplifying equations defined as:

Parameter Extraction
As is customarily the case for any networks in which the equivalent circuit can be defined via lumped-elements using simple analytical formulations, the model parameters are extracted directly from measured (intrinsic) data by determining the slope and Y-intercept of the constituent real and imaginary parts. In the case of the SVIA, the series impedance is expressed by Equation 2, assuming that ω2Lvia2 << 1.

Rvia is extracted graphically from a plot of real (Zseries) versus ω2, by finding the y-intercept of the data. Lvia is extracted graphically from a plot of imag (Zseries) versus ω by finding the slope of the data. In the case of the MIM cap, the series impedance is expressed by Equation 3, assuming that ω2Ls2/Rp << 1.

Using similar graphical extraction methods to those used in the modeling of the SVIA, Cs is extracted graphically from a plot of ωimag (Zseries) versus ω2 as the y-intercept, where Ls is extracted from the slope of the same data. Rs is determined from the y-intercept of the real (Zseries) versus ω2 data. Having determined Ls, Rp is determined by dividing ω2Ls2 by the slope of the real (Zseries) versus ω2 data. Extraction of the shunt/substrate model parameters is accomplished from the LE-EC in a similar manner via the definition of the equivalent substrate admittance Ysub.5
(On-Wafer) Calibration and Verification
An on-wafer SOLT calibration is utilized as the basis for characterization, because it has been found to provide the most accurate results at the very low frequencies where the impedances associated with the (electrically) largest devices are extracted. Standards should be designed such that the reference plane is defined at the center of the RF padframe housing the (physically) largest DUT. An on-wafer TRL calibration is first performed in order to establish the electrical equivalents (calibration kit constants) for the SOLT standards. In order to support the measurement of the ultra low resistances associated with the DUTs, it is critical that the TRL calibration be verified through the measurement of the SOLT load (match) standards at each port. Proper adjustment of the capacitance associated with the transmission line standard insures that DC and RF derived resistances of the load (match) standard are in agreement. (This procedure is readily facilitated in WinCal XE). Once the calibration has been performed, it is verified using both a standard re-measurement procedure1,6 as well as through measurement of independent standard devices.
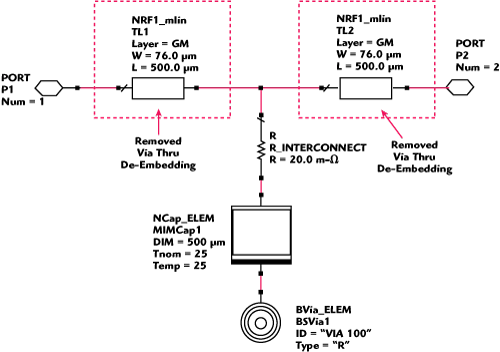
Figure 7 "Series-shunt" MIM cap two-port thru-de-embedding configuration.
Thru De-Embedding
The measurement configuration of the series-shunt connected MIM cap is shown in Figure 7. Parasitics associated with the microstrip transmission lines, which extend from the center of the MIM cap to each of the calibration reference planes, are removed via a Thru de-embedding procedure, which utilizes cascaded ABCD matrix methods. (This is identical to the use of reciprocal two-port networks in ADS). Data for the embedding transmission line sections is obtained either via EM (Momentum) simulation or via splitting7 the S-parameter data measured on the Thru calibration standard. The de-embedding process proceeds according to the illustration shown in Figure 8.8

Figure 8 Cascaded ABCD de-embedding methodology.
Procedurally, (1) the measured data is converted from S into ABCD format, (2) the DUT is de-embedded (using cascaded ABCD matrices, or via ADS) and (3) the residual (intrinsic) data is converted from ABCD format back into S.
Measurement Results
Measured data for the "series-shunt" connected SVIA presented previously showed good agreement with statistically derived values for Rvia (χ = 21 m-Ω) and Lvia (χ = 34.5 pH),1 with both parameters demonstrating normally distributed characteristics, as shown in Figure 9.

Figure 9 SVIA Rs (a) and Ls (b) distributions.

Figure 10 MIM cap real (Zseries) vs. ω2.
Typical data for the series-shunt configured MIM cap is shown in Figure 10. For the 37.5 pF capacitor, it is noted that extraction of Rs from de-embedded Real (Zseries) data is valid over the range of approximately 900 MHz < freq. < 2 GHz. Below this frequency, the measurement accuracy begins to degrade as a result of the VNA's inability to resolve the resistance from the effects of the ever-increasing, significantly larger, reactive signal component associated with Cs.
Validation
Validation of the modeling technique is demonstrated in terms of the statistical data obtained as a result of application of the combined de-embedding and parameter extraction methodologies during characterization of multiple 37.5 pF square MIM capacitors. The summary provided in Table 3 results from data taken via automatic probing on six co-located die from the same wafer.
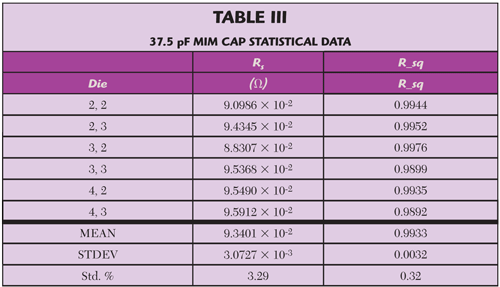

An error well less than five percent (2.6 m-Ω), between the measured and estimated MIM resistance, results by recalling the sum of the via and interconnect resistances (per Table 2.) as is shown in Table 4. Further validation of the device characterization and associated MIM cap modeling methodology comes in terms of playbacks of Cs, Rs and Q11 seen in Figures 11 through 13.9 The data shown was generated on rectangular MIMs from TQP15.
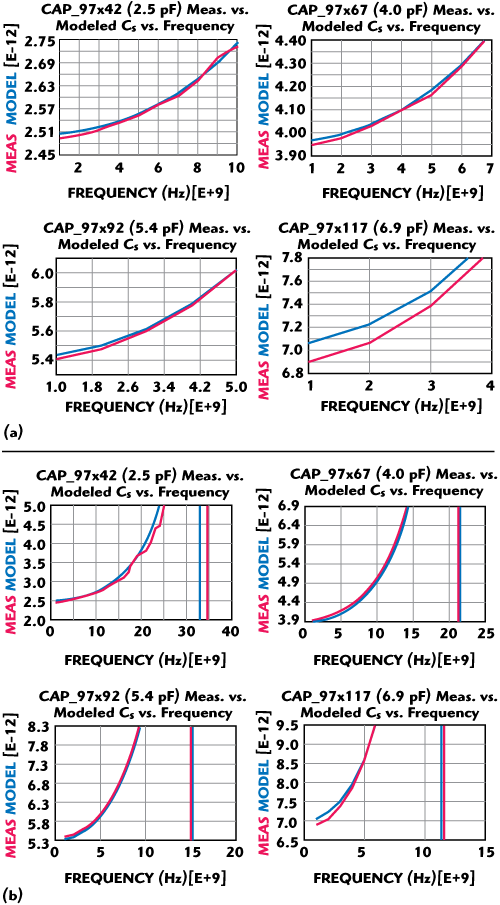
Figure 11 (a) (Close-in) vs. frequency and (b) (far away) Cs vs. frequency.
The accuracy associated with the extraction of Cs can be seen in the plots of Cs versus frequency (Figure 11a), where a narrow bandwidth is displayed. The accuracy associated with the extraction of Ls can be seen in the plots of Cs versus frequency (Figure 11b), where a wider bandwidth is displayed. The accuracy associated with the extraction of Rs can be seen in the plots of Cs versus frequency (Figure 12) where a wider bandwidth is displayed. The accuracy associated with the overall model extraction process can be seen in the plots of Q11 versus frequency in Figure 13. The impact of fitting errors associated with both the real and imaginary parts of Zseries are displayed over the full characterization bandwidth of 50 GHz.

Figure 12 Rs vs. frequency.
Conclusion
A methodology, developed for determination of the series resistance of SVIAs, has been successfully applied to the characterization of MIM Caps. The methodology has shown that the resistance of MIM Caps can be readily obtained from measured S-parameter data through: (1) the design/use of "series-shunt" configured test structures, (2) application of the "S21-shunt" ultra-low impedance measurement technique, and (3) proper VNA configuration/setup. The series resistance for a large, square geometry MIM cap that has been extracted directly from measured S-parameter data (based on the use of slope and intercept methods), compares well with data obtained with other, similar modeling procedures.10 Data taken on six die clearly demonstrates that the effects of probe contact resistance (PCR) and its associated variability have been eliminated as sources of measurement error and statistical variability.

Figure 13 Q11 vs. frequency.
Acknowledgments
The work presented in this article was done while the author was employed at Nitronex Corp. I would like to thank John Kearney for layout of the test structures, and would also like to acknowledge Prity Patel for her effort in the construction of the on-wafer calibration kit as well as during collection of the associated S-parameter data.
References
- M.D. Brunsman, "Through-Wafer Via Modeling Based on Direct RF Characterization," 76th ARFTG Microwave Measurements Conference, Clearwater, FL, Paper C-1, 2010.
- "Ultra-Low Impedance Measurements Using 2-Port Measurements," Agilent Technologies Application Note 5989-5935EN.
- "RF Probe Selection Guide," a publication of Cascade Microtech.
- Liu Lianto, et al., "A New Equivalent Circuit Model of MIM Capacitor for RFIC," 2007 International Conference on Microwave and Millimeter Wave Technology Digest, pp. 1-3.
- Seong-Sik Song, et al., "Simple Wide-Band Metal-Insulator-Metal (MIM) Capacitor Model for RF Applications and Effect of Substrate Grounded Shields," Japanese Society of Applied Physics, Vol. 43, No. 4B, 2004, pp. 1746-1751.
- M.D. Brunsman, "Verification of On-Wafer (SOLT) Calibration," Agilent EEsof EDA publication 5989-9467EN.pdf, September 2003. http://cp.literature.agilent.com/litweb/pdf/5989-9467EN.pdf.
- M.D. Brunsman, "De-Embedding Series-Connected/Transmission Configured Devices," Agilent EEsof EDA publication 5989-9466EN.pdf, March 27, 2008. http://cp.literature.agilent.com/litweb/pdf/5989-9466EN.pdf.
- X. Shi, et al., "Characterization and Modeling of On-Wafer Single and Multiple Vias for CMOS RFICS," Microwave and Optical Technology Letters, Vol. 50, No. 3, March 2008, pp. 713-715.
- R. Sanusi, et al., "Scalable MIM Capacitor Polynomial Equation Model Development with Application in the Design of 2.4 GHz PHEMT Low Noise Amplifier," 2009 Asia Pacific Microwave Conference Digest, pp. 2518-2521.
- A. Mellberg and J. Stenarson, "An Evaluation of Three Simple Scalable MIM Capacitor Models," IEEE Transactions on Microwave Theory and Techniques, Vol. 54, No. 1, January 2006, pp. 169-172.
