Today's engineer faces a range of challenges, including inadequate nonlinear device models that contribute heavily to inaccurate large-signal high frequency simulation. Because of this, designers need to know if a model they are given is suitable for their application before they commit a design to manufacture. Unfortunately, the hurdle for pre-qualifying a nonlinear model is often perceived as high, so few engineers will even ask the question: "Is my model good enough?" Failure to accurately take into account the dynamic behavior of a device in its electrical model can have a detrimental effect on an application. Therefore, modeling such behavior is essential to accurate nonlinear simulation.
A powerful simulation-based qualification method now offers designers a viable means of testing field-effect transistor (FET) device models for critical large-signal, high frequency behavioral characteristics at the operating point required by an application. This early insight is critical in allowing designers to avoid costly and time consuming design iterations and their consequences.
Understanding Dynamic Behavior
To better understand why taking a device's dynamic behavior into account is so critical, it is first important to understand exactly what this behavior is. Dynamic behavior occurs when an object gives measured results that are a function of when a change started (implying memory of past conditions) and/or for how long the change was applied (process/mechanism time constants). It may be exhibited by all semiconductor devices in response to appropriate changes in electrical stimuli, but is particularly prevalent in applications where large-signal, high frequency signals are present (that is RF power amplifiers, mixers, oscillators and high speed digital circuits). Device technology and size do impact a device's dynamic behavior, but it is unreasonable to assume that an application employing the latest deep sub-micron silicon process will be any less likely to exhibit dynamic behavior than a 50 W GaN device.
Essentially, when a device in a quiescent (steady) state experiences a change in electrical conditions, that change does not instantly result in a new steady-state condition. Rather, physical processes, each with differing time constants, begin to respond. The observed result is a time variant change in the electrical conditions observed at the device terminals.
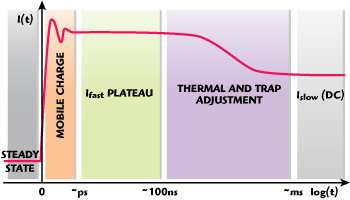
Figure 1 I(t) changing response to a step change in voltage at t = 0.
Consider the case shown in Figure 1, which depicts an Id(t) response of a FET to a step change in applied voltage. After t = 0, the mobile charge in the channel responds rapidly and then I(t) settles down to the "Ifast Plateau" current region. Next, the change in conditions affect the channel temperature and, in some device technologies, the charge state of traps (dislocations/imperfections in device material lattice that show up as discrete energy levels in the material band gap). In turn, changes in channel temperature and trap states affect the apparent mobility of carriers in the channel and cause the current flow to adjust until it reaches equilibrium (Islow). This change over time can also be viewed as the device responding in a different way to different applied frequencies or dispersion.
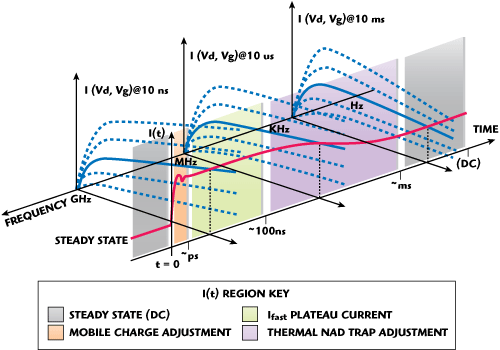
Figure 2 The step response relationship between I(V) and I(t).
The relationship between I(V), taken at different effective pulse lengths, and the step response in Figure 1 is shown in Figure 2. Note that the device I(V) characteristic measured at "DC" is not the same I(V) characteristic seen by a high frequency signal.
From the I(V) curves in Figure 2, it is possible to infer that derivatives of I with respect to V are time dependant. Consider the partial derivative ∂id/∂vg, or gm. Clearly the gain will be different for a high frequency signal compared to a slow moving one. Likewise, harmonic generation and intermodulation products are dependent on I-V derivatives and so are other key quantities like ACPR, AM-PM, EVM and PAE. An inappropriate model description for the rate dependence of the I-V plane will produce incorrect answers for these critical metrics.
Modeling Dynamic Behavior
While several approaches have been developed to allow the inclusion of dynamic behavior in semiconductor device models, determining if a model is well fitted to appropriate measured data remains challenging. A model only fitted to DC I(V) and quasi-static S-parameters is highly unlikely to give accurate large-signal, high frequency performance. Large-signal high frequency information must be used as part of model fitting. Moreover, large-signal high frequency simulated tests are needed to evaluate how well a model has been fitted.
Simulated testing of a FET device model for large-signal, high frequency behavior, can be carried out in many ways. The easiest, quickest and most insightful method is to test the dynamic capabilities and fit of a model by comparing DC I(V) with fast-pulse i(v). Examining critical areas of a fast-pulse i(v) characteristic can yield vital information on the general suitability of a model for a given task. For example, it can determine if appropriate dynamic behavior is modeled, if the model is well fitted for large-signal high frequency use in a specific application, and examine the model's valid range of use.
It may also be useful to look at the device's step response characteristic i(t) to see if it behaves rationally. Pre-configured simulation testers and measurements, like those available for Agilent Technologies' Advanced Design System software, make it possible to quickly and comprehensively look at a device's time-dependant behavior. Three such tests are the single shot pulse i(v), continuous time pulse i(v) and step i(t). With the single shot pulse i(v), equal length pulses, starting from the Q-point, are sent simultaneously to both gate and drain terminals. Terminal currents are then measured at a user defined intra-pulse sample point to provide the fast-pulse i(v) values for plotting. Continuous time pulse i(v) uses the same basic methodology except that each pulse is applied as part of a single time sweep, rather than individual per pulse time sweeps. In a step i(t) tester, terminal voltages are simultaneously changed from the Q-point to a desired "step-to" point and held for the duration of the test with terminal currents monitored over time.
Testing a Model Using Fast-Pulse Simulation
A number of qualitative tests can be used to check the primary characteristics of a model related to dynamic behavior. While these tests do not guarantee accurate circuit simulation results, they will quickly identify suspect model behaviors that require further investigation. These tests include:
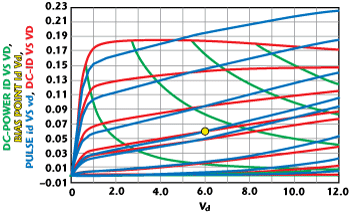
Figure 3 I-V plane showing DC I(V), pulsed i (v) and DC power curves.
Output Conductance
The I-V plot in Figure 3 shows differences between the DC I(V) (red) and pulsed i(v) (blue) and DC power (green) curves. Examining the pulsed i(v) set above the knee shows a relatively constant positive value of output conductance for all constant vg traces. The DC I(V) set shows differing values of output conductance across the plane, with negative values at higher power dissipation. This difference is the result of the DC I(V) curves containing a "hidden" dependence on channel temperature and trap state.
Overall Shape of i(v) Curves (Q-Point Dependence)
For any given bias Q-point, the combination of power dissipation and the charge state of traps is unique. The shape of the pulsed i(v) curves will vary according to that Q-point. The ability to track this critical behavior is a major challenge for a device model. Some models are fitted to data for a specific characterization Q-point and only accurately replicate the device's dispersive behavior when operated at that Q-point. Using the model at an operating point away from that Q-point usually leads to a degraded characteristic. How important this degradation is to overall accuracy is application dependant. Few, if any, empirical models are able to accurately cover the general case and, if not fitted using data from multiple Q-points, will be inaccurate.
Pinch-Off
As with the DC I(V) characteristics, the pulsed i(v) results should show the device pinch-off as a function of gate voltage. Generally speaking, while the values of Vg at pinch-off may differ, and the shape of the curves may be different approaching this region, the device model should still pinch-off to Id = 0 for both DC and pulsed data.
Drain Current Offset at the Origin
Some device models cannot accurately predict behavior away from their pulsed i(v) characterization bias. This can be seen in an offset at the origin of the pulsed i(v) curves. In cases where an obvious offset can be seen, the designer must examine the effect of this artifact on the target application.
Bias Point
The coincident nature of the bias point on both DC I(V) and pulsed i(v) characteristics is a given. This condition is both logical and necessary because the DC I(V) characteristic is effectively the set of quiescent bias points from which any pulse measurement can be taken.

Figure 4 Gm curves from DC and pulsed simulations.
Transconductance – Gm
The differences between DC and pulsed measurement values of Gm are readily apparent in Figure 4, and highlight the importance of correctly modeling the dispersive nature of a device. Higher order derivatives, which give indications as to intermodulation products and harmonic generation, also behave in similar ways.
Memory Effects
When a device's response is dependent on its operating history, it is said to "remember" the past and hence, has memory effects. For a device model without any memory capability, simulation results will be identical for a given point on the pulse i(v) plane, irrespective of the number of pulses, their order or coverage of the I-V plane. This is not true for a device exhibiting memory, where the same pulse stimulus conditions can result in different responses.
Step Response
This test looks for the behavior shown in Figure 1. It also tests the time constants associated with a particular device or its model. This test is often performed to make sure the simulated fast-pulse i(v) measurements use a sufficiently fast pulse to correctly characterize the high frequency plateau described in Figure 1.
Conclusion
Taking into account the dynamic nature and behavior of a FET device in any electrical model is essential for accurate nonlinear simulations. Fortunately, designers can now use a powerful simulation-based qualification method to test FET device models for critical, large-signal high frequency behavioral characteristics at an operating point required by their application. Additionally, straightforward qualitative simulated tests can be used to quickly test the "goodness" and fit of the dispersive behavior of a given FET model. Such early insight is critical to avoiding costly, time-consuming problems at a later date.

Graham Riley received his B.S. in Communication Engineering from Plymouth University and a M.S. in Microwaves and Modern Optics from University College London. He is an Application Engineer for Agilent Technologies' EEsof EDA organization, with more than 20 years of experience in the use and application of analog, RF and microwave EDA software.
