Optimization has been applied to circuit design for decades. IBM pioneered circuit simulation-based optimizer research in the 1960s and ’70s. In the 1980s, the University of California at Berkeley extended the research with more exotic algorithms and interactivity with programs such as DELIGHT and ECSTACY. During the same period, AT&T Bell Labs, using a program called TILOS, used optimization for transistor sizing of custom digital circuits in order to improve timing performance. Today, optimization products can be obtained from most major electronic design automation (EDA) providers.
Microwave designers have traditionally applied optimization widely to improve and center the performance of their circuits. However, even though optimization has long been an established workhorse for microwave designers, its application in analog integrated circuit (IC) design has been hampered by poor ease-of-use and performance. This tutorial describes a fast, easy to use and highly interactive optimization solution that is very effective for analog and RF/microwave applications.
As opposed to some circuit optimizers on the market that require tedious setup and run mostly in a batch mode, the solution described in this article is designed for easy setup and interactive use during the circuit design creation process. While many solutions offer just one algorithm, this one offers a number of different optimization algorithms and methods that can be applied depending upon the problem definition and breadth of the design space to be explored. Many of these algorithms begin at a user-defined starting point and search the design space from that point to find the local optimum. Some, like Genetic and Pointer, can search the entire design space to find the global optimum. These particular algorithms can even handle discrete component and sub-circuit choices that can be used to synthesize circuit structure. Some of the unique and powerful features of this optimization solution are demonstrated in the following example. A list and descriptions of all the algorithms included are shown in Appendix A.
Design and Optimization of a High Frequency Operational Amplifier
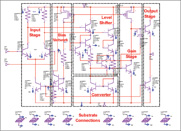
The schematic of the amplifier to be optimized is shown in Figure 1. The application is to amplify intermediate broadband signals up to 2 GHz. As an operational amplifier, it will always be used in a closed-loop configuration, which is a real challenge at these frequencies. Consequently, it is imperative that the phase shift through the amplifier be kept to a minimum. Because of the high frequency requirements, the amplifier will use a leading foundry 60 GHz silicon germanium technology. In this technology, the NPN bipolar transistor is the active device of choice, since all other transistor types are significantly lower in performance. Therefore, the signal path is kept simple and mostly NPN-based except for one P-channel metal-gate transistor (PMOS) load device. The architecture of the circuit is typical of most operational amplifiers and is made up of the following building blocks:
• Input Stage – a classical differential transistor pair gain circuit driving matched resistive loads and biased by a current source.
• Voltage Level-shifter – differential emitter-followers that drive diode- and resistor-level-shifters into a differential-to-single-ended converter.
• Differential-to-single-ended Converter – as the name implies, this circuitry converts the differential voltage through the level-shifter to a single-ended signal.
• Common emitter Gain Stage with PMOS current source load. This stage is driven by the output of the converter and generates most of the gain of the amplifier.
• Emitter follower Output Stage with NPN current source bias – this stage buffers the gain stage high impedance node from the output load.
• Bias Network – this relatively simple circuitry establishes all the current sources in the amplifier. A more complex bias network could significantly reduce the variability of the amplifier over power supply changes, but that is an exercise for another time.

Figure 2 is a view of the optimized amplifier layout.
Design Project Setup
Setting Up Test Benches and Corners of Interest
The operational amplifier project is configured into three test benches — one each to measure DC, AC and transient performance specifications. The amplifier is also rated to operate over positive power supply voltage corners of 3.7 to 4.3 V and a load capacitor range of 0 to 1 pF. Accordingly, parameter sweep blocks are included in all the test benches for the power supply and load capacitor. Any number of parameter sweeps can be defined, including temperature and process corners.
Defining Measurements and Optimization Objectives/Weights
For this amplifier, the goal is to meet or exceed the bandwidth and gain requirements, while at the same time minimizing power and maintaining stability. As might be expected, these are very conflicting requirements. Designers can spend many tedious hours and even days trying to meet specifications, much less finding the best solution. Often, in the interest of time, designers will settle for an acceptable solution without pushing the design for all it can deliver. This is where optimization can really pay off. In addition to the bandwidth, gain, power and stability, numerous other requirements must be considered. In this example, power supply rejection ratios and preferential DC offset are included in the optimization trade-offs. Most of these goals are either inequality constraints that should be less or greater than a target value or line segment. There is one equality objective to ensure that the amplifier is free of any preferential DC offset voltage. Other measurements are monitored but not included as objectives.

Once measurements are defined, setting up the optimization objectives is very easy. As shown in Figure 3, when choosing “Add an Optimization Goal,” a form pops up displaying all the measurements. The user simply selects which measurement to include in the optimization session and chooses whether to make it greater, less than, or equal to a value (or range of values over a frequency or time range, if applicable). In this example, the optimization goals are evaluated using a variety of simulators:
• For the DC operating conditions, including power and output offset voltage, the harmonic balance simulator is used.
• For the AC performance factors, including open- and closed-loop small-signal gain and phase as well as the positive/negative power supply ratios, the linear simulator is called.
• For the time-domain unit-step overshoot calculation, Synopsys’ HSPICE transient analysis is executed.
Note that simultaneous optimization of goals from different simulators is a unique feature not offered in all circuit design tools.
Using experience and first principles, some time was spent to tune and refine an initial set of component values. With the touch of one button, all measurements are evaluated and, at the same time, those measurements associated with the optimization session are included in the overall cost function value. By defining the optimization goals with corner sweeps, the optimizer will ensure that the worst-case corner measurement is always considered during the session. This feature provides a form of design centering. In all, four HSPICE transient simulations and four DC and AC frequency-sweep simulations are run, taking about 20 seconds on a 1.4 GHz Pentium PC. Obviously, keeping simulation time to a minimum is an important factor in speeding up the optimization session.

Listed below are the specific objectives to be considered during the optimization session, as shown in the Optimizer Form (see Figure 4).
• The first Open-loop Gain objective is the amplifier low frequency open-loop gain (magnitude) that should be greater than 400.
• Vout Mag (a measure of stability) is the AC closed-loop gain peaking between 0.5 and 10 GHz that should be less than 14.
• PSRR is the positive power supply rejection ratio up to 0.01 GHz that should be less than –50 dB.
• NSRR is the negative power supply rejection ratio up to 0.01 GHz that must be less than –50 dB.
• Power is the amplifier DC power that must be less than 60 mW. However, to push for lower power, a very challenging 40 mW is targeted.
• The next Open-loop Gain objective is a measure of the Gain-bandwidth product and should be greater than 12 at 1 GHz.
• Phase Neg is the phase shift through the amplifier and should be less than 60° at 2 GHz and less than 300° at 10 GHz. This constraint is not actually required, but was added to keep the amplifier from becoming unstable. It will not be included in the trade-off analysis to come.
• Vout is the DC output voltage and a measure of the preferential offset voltage. It should be equal to 2 V, the input common mode voltage.
• Transient Overshoot (a measure of stability) is the pulse response output overshoot in the time domain and should be less than 0.02 V (~20 percent).
To ensure a successful optimization session, it is important that the user define realizable goals and constraints. There is nothing wrong with pushing the envelope, but setting grossly unachievable objectives will only reduce the effectiveness of the optimizer. If the user finds that some of the targets are too aggressive, refining them during the optimization session is possible and can enhance the ultimate solution.
The amplifier optimization goals and constraints were set after running an initial set of measurements. Notice in the Optimizer Form that the “Cost” values are all about the same as a consequence of selecting the “Equalize Goals” command. When necessary, weights can and should be modified to increase or decrease the objectives’ importance in the overall cost metric. When invoked, the optimizer will modify the design parameters to reduce the overall cost value. The cost value is a relative measure of goodness and is only pertinent when compared to other costs in the same session.
When dealing with a large number of requirements and design parameters, there should be no illusion that there exists only one best set of design parameters. There are a variety of component value combinations that can give similar results, and more importantly, defining what “best” means is usually a very subjective exercise. That is, meeting or exceeding the requirements as shown on a data sheet is very definitive. But, what if the DC power could be reduced significantly with only a marginal degradation in other performance factors. Would that be better? Only the specific system application for the amplifier can answer this question. Therefore, offering a variety of performance options to the system designer may be the best approach, and again, the optimizer is the best way to quickly generate these options.
At any time, the optimization session can be interrupted so that goals, measurements, design parameters, test benches and circuit topologies can be modified. The session can then be restarted from the last design state or any previously saved state. This ability to interact with and modify any aspect of the problem during the session is crucial to the effectiveness of the optimization. It offers the designer the flexibility to use his/her knowledge of the design to refine the problem and search to better the results.
Selecting Design Parameters and Setting Their Initial Values/Constraints
Intelligent selection of the goals and their weights/targets is only part of the path to a successful optimization session. Probably more important is the selection of the design parameters, their initial values and min/max constraints. Some optimization tools promote the fact that they can handle very large numbers of parameters without much insight as to their impact on the goals or their initial values. However, by simply throwing every design parameter with an arbitrary value into the mix, the optimization session is sure to be more time-consuming and unproductive. The optimizer solution described here can also handle large numbers of design parameters, and the algorithms available are very robust. Most can usually find a good solution from any reasonable starting point. Here again, it is the designer’s knowledge of the problem that can best be applied to pick a thoughtful and manageable set of design parameters and their starting values. In IC circuit design, the selection of design parameters is made more interesting because some component values must “match” others, and some have only discrete choices. Defining “matched” component values is easily done by creating a single variable for those values. The variable is then defined as an optimization parameter. To define a discrete parameter, the component value is simply made into an integer variable and the optimization algorithm then recognizes it as such. Two of the 10 built-in algorithms available, Pointer and Random, will support combined discrete and continuous variable optimization. For this operational amplifier example, the design parameters selected for the optimization session are shown in Figure 5, where

• RE is the length of the level-shifter matched resistors whose values help define the voltage and current levels of the level-shifter, that is, power, gain and offset voltage.
• RBias is the length of the bias resistor defining the currents throughout the amplifier, that is, power, gain, gain-bandwidth and stability/phase shift.
• RL_in is the length of the input stage matched load resistors that affects gain, level-shifter voltages and phase shift.
• QinL is the discrete matched parameter for the input stage device sizes whose emitter resistances and parasitic junction capacitors help determine gain, bandwidth and stability/
phase shift.
• Q3_LENGTH is a discrete parameter for the input stage current source device size that determines the input stage current and partially determines its transconductance, that is, gain and power.
• Q12_LENGTH is a discrete parameter device size for the gain stage transistor whose current density, parasitic capacitance and emitter resistance is central in the calculation of gain, gain-bandwidth and stability.
• C1_W is the gain stage compensation capacitor width that determines the roll-off capacitor value, that is, gain-bandwidth product and stability.
• M2_WF is the finger width of the PMOS device that determines the gain stage load current source value, that is, gain and power.
There are numerous other component values that could be included, but most of them have only second-order impact upon the goals. After setting the initial values, some manual interactive tuning was applied to bring the design to a reasonable state that comes close to meeting the critical requirements. However, when dealing with more than a few requirements and design variables, it is very difficult to find the best solution. This is where optimization is best applied.
Constraining the design parameter excursions is always a good idea. Keeping capacitor and resistor values above zero and less than what the semiconductor process can deliver is probably obvious. But it is also good practice to limit the range of the design parameters even further to keep the optimizer from considering cases that are clearly unacceptable.
The Optimization Session
Selecting the Algorithm and Testing the Design Space
Now that the goals, weights, design parameters and constraints are defined, the optimizer is ready to run. Since this amplifier has discrete design parameters, either the Pointer or Random algorithm can be applied. The Pointer algorithm is chosen because it is typically more efficient for nonlinear problems with costly simulation run-times. Before the optimizer is let loose to run a lengthy session, it is advisable to see how the design improves over a small number of iterations (25 to 50, for instance). If no improvement is seen, it should be run a little longer, and if there is still no change, it may be necessary to modify the setup by changing weights, goals or design parameters. It may even help to add or eliminate goals or design parameters. In most cases, the user will see some measurable improvement and the optimizer can then be run for a much larger number of iterations to realize a much better design.
Running the Optimizer
The optimizer is run for 50 iterations and the results analyzed. After 50 iterations, the cost function is improved substantially. Once it seems that things are set up properly, the optimizer is run for a total of 100 iterations. This takes about 30 minutes. At this point, the objective weights were refined to improve power at the expense of some of the other requirements. Also, some design parameters were disabled after they were seen to diminish in importance as the session proceeded. This process continued with incremental 100 iteration runs/refinements to understand and generate options between the overall trade-offs. This interaction is vital to maximize the optimization. In total, the session takes several hours, but the designer can be confident that the design space trade-offs have been comprehensively covered and the performance of the amplifier has been pushed to its limits.

Results of the Optimization Session
Table 1 shows the results of several different optimization sessions for the operational amplifier. The worst-case objectives were measured at 50, 100 and 300 iterations with emphasis on low DC power. Another 300 iterations with emphasis on high speed or gain-bandwidth product were then taken. As can be seen, the optimizer was able to deliver significant improvement in the most critical specifications, while maintaining reasonable values for the others.
Conclusion
Although many EDA companies offer optimization, the technology has not progressed very rapidly in the analog circuit design world and most tools are limited by poor ease-of-use, tedious setup and slow performance. This tutorial has demonstrated an easy-to-use, fast and interactive optimization solution that works very effectively for analog and RF applications. The solution discussed in this article provides a highly efficient alternative to the traditional process that employs multiple optimization algorithms and provides a choice in methods that can be applied depending upon the problem definition and breath of the design space to be explored.
James Spoto received his BS and MS degrees in electrical engineering from the University of Florida. He is currently president and CEO of Applied Wave Research Inc. (AWR). Prior to joining AWR in 2001, he was a senior executive at Conexant Systems. He is a member of the IEEE and Tau Beta Pi.
