Dielectric resonator antennas (DRA) are a relatively recent addition to antenna technology and have been the focus of increasing research activity over the last two decades. A DRA is a resonant antenna fabricated from low loss microwave dielectric material whose resonant frequency is predominantly a function of size, shape and material dielectric constant. In its fundamental mode of operation, a DRA will radiate like a short magnetic or electric dipole. A good review of the radiation characteristics of DRAs of basic shapes is found in Mongia, et al.,1 while more recent advances are highlighted in Petosa, et al.2
Much of the research findings are contained in the first book on DRAs.3 The main advantage of this antenna technology lies in its versatility. The wide range of available DRA shapes, dielectric constants and feeding techniques gives these antennas the flexibility to conform to the physical and electric requirements of numerous applications.
Although much of the investigation has focused on characterizing or enhancing the performance of individual elements, some research has also considered the DRA in an array environment. The multi-segment DRA4,5 and the perforated DRAs6 are examples of new developments in DRA technology designed to facilitate their use in large arrays. With the push towards higher frequency communications, and using technology such as low temperature co-fired ceramics (LTCC) or micromachining, arrays of low loss, low cost DRAs at millimeter-wave frequencies are a realistic goal.
DRAs are still at an early stage of development, but they are beginning to find their way into commercial products such as in handsets, laptops and Bluetooth devices. The intent of this article is to assist the antenna engineer in the design or analysis of rectangular DRAs. It also provides a useful tool to the system engineer for quickly obtaining the practical range of antenna dimensions for a given frequency and bandwidth, which would aid in the design layout of a system.
Rectangular Dielectric Resonator Antenna
Although DRAs can take on many shapes, the two most common are cylindrical and rectangular. Simple design equations for predicting the resonant frequency and radiation Q-factor of various modes of cylindrical DRAs have been presented previously,1,7 based upon both the dielectric waveguide model and on intensive numerical analysis. Useful graphs of the normalized frequency and Q-factor as a function of the aspect ratio of the cylindrical DRA are also provided in Kishk, Glisson and Junker.7 In this article, a set of curves is presented for determining the resonant frequency and radiation Q-factor of the lowest order mode (TE11?) of a rectangular DRA. These curves can be used to either analyze a rectangular DRA of given dimensions, or as a design tool to determine the DRA dimensions for a desired resonant frequency.
The geometry of the rectangular DRA is shown in Figure 1. The DRA has a relative dielectric constant of er, and is oriented with the dimension a parallel to the x-axis, d parallel to the z-axis and a height h. In the majority of cases, the DRA is mounted on a ground plane and can be excited using various standard feeds such as probes, apertures, or direct coupling to microstrip lines. A fairly accurate model for predicting the resonant frequency and radiation Q-factor of an isolated DRA (which is equivalent to removing the ground plane and doubling the DRA height: b = 2h) is based on a truncated dielectric waveguide.8 To determine the frequency of the isolated DRA using this model, a transcendental equation must be solved. Although this is not difficult to do, it does not lend itself readily to design. Therefore, following an approach similar to that taken in Kishk, et al.,7 a set of design curves has been generated which plot the normalized frequency and radiation Q-factor for a range of aspect ratios of the rectangular DRA. These curves are convenient for quickly estimating the resonant frequency and Q-factor of a DRA of specific dimensions and dielectric constant, or they can be used to quickly compare the Q-factor of rectangular DRAs having the same resonant frequency but different aspect ratios or dielectric constant.

Fig. 1 Geometry of the rectangular DRA.
Resonant frequency
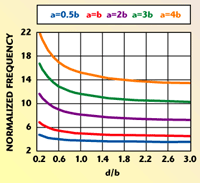
Fig. 2 Normalized resonant frequency of a DRA as a function of its aspect ratio.
The resonant frequencies for various aspect ratios of the rectangular DRA have been determined by solving the transcendental equation given in Reference 8. The results are plotted in a set of curves shown in Figure 2. The curves plot a normalized frequency, F, of the TE11? mode, as a function of different aspect ratios. F is given by

where f0 is the resonant frequency in GHz of the isolated DRA and a is expressed in units of mm. The curves can be used for either analysis or design. In analysis, the resonant frequency of the DRA is determined for a set of given dimensions and dielectric constant. For example, consider a cube DRA mounted on a ground plane with dimensions a = h = b/2 = d = 10 mm, and a dielectric constant of ?r = 20. The resonant frequency is determined by choosing the value of F corresponding to the intersection of d/b = 0.5 with the curve for a = 0.5b (since h = b/2). Thus, F = 4.1, and solving Equation 1 for f0 results in a resonant frequency of f0 = 4.38 GHz.
The same figure can also be used to determine the dimensions of a rectangular DRA for a given resonant frequency. One of the main advantages of a rectangular DRA is its degree of freedom. For a given dielectric constant there are numerous practical combinations of the DRA dimensions, which will result in the same resonant frequency (although they will not necessarily have the same radiation Q-factor, as will be seen later). For example, the design of a DRA with a resonant frequency of 10 GHz and dielectric constant of ?r = 15 is considered. From Equation 1, F = 0.81116 a. A value for d/b is then selected. From the curves shown, the values of F are found for each corresponding a/b curve. From these values of F, a is determined, then b and d follow. To illustrate, d/b is chosen to be 1.5. Table 1 shows the values of F read from the figure for each of the a/b curves and the corresponding final dimensions. This could be repeated any number of times using different values for d/b and allows the designer to quickly get an idea of the range of DRA dimensions which will resonate at the desired frequency for a given dielectric constant.

Radiation Q-Factor
The radiation Q-factor of a rectangular waveguide can also be obtained from the dielectric waveguide model and is again based on solving the original transcendental equation for resonant frequency.8 Unfortunately, the Q-factor cannot be plotted as concisely as the resonant frequency, and separate graphs are required for each of the five a/b ratios shown. Figures 3 to 7 plot the normalized Q-factor, Qe, as a function of d/b ratio for various dielectric constants. The normalized Q-factor is given by

Following up with the earlier analysis example, the radiation Q-factor of the cube DRA with dimensions a = h = b/2 = d = 10 mm and a dielectric constant of ?r = 20 would be found by using the figure for a/b = 0.5. The value of Qe is found from the intersection of the d/b = 0.5 and the er = 20 curve. Qe = 0.181 and using Equation 2, Q is 16.2. The bandwidth, BW, of the DRA can then be determined from

where s is the desired voltage standing wave ratio. In this example, for
s = 2, the bandwidth would be 0.044 or 4.4 percent.

Fig. 3 Normalized Q-factor as a function of d/b for a/b=0.5. | 
Fig. 4 Normalized Q-factor as a function of d/b for a/b=1. |

Fig. 5 Normalized Q-factor as a function of d/b for a/b=2. | 
Fig. 6 Normalized Q-factor as a function of d/b for a/b=3. |

Fig. 7 Normalized Q-factor as a function of d/b for a/b=4. |
In a similar manner, the radiation Q-factors can be determined for the five cases of rectangular DRAs resonating at 10 GHz, and these are listed in Table 1. For s = 2, the bandwidths for these resonators range from 6.2 percent (for Q = 11.4) to 11.6 percent (for Q = 6.1). This simple design example illustrates the flexibility in choice of rectangular DRAs and how the curves for normalized frequency and radiation Q-factor can be used by designers to quickly assess the tradeoffs between DRA dimensions and bandwidth.
Conclusion
Design curves based on the dielectric waveguide model for isolated rectangular DRAs have been generated for determining their resonant frequency and radiation Q-factor. These curves can be used for the analysis or design for either isolated rectangular DRAs or for DRAs mounted on ground planes (by using h = b/2). One point that should be emphasized is that the dielectric waveguide model does not include the effects of the excitation mechanism and the presence of this feed may impact the resonant frequency and Q-factor of the DRA. Also, the accuracy of the model for extreme aspect ratios (very tall and skinny or very large and flat) has not been verified and caution should be taken when using the curves in these regions. Nevertheless, this model can be used as a good starting point for the design or analysis of rectangular DRAs.
References
1. R.K. Mongia and P. Bhartia, “Dielectric Resonator Antennas – A Review and General Design Relations for Resonant Frequency and Bandwidth,” International Journal of Microwave and Millimeter-wave Computer-aided Engineering, Vol. 4, No. 3, 1994, pp. 230–247.
2. A. Petosa, A. Ittipiboon, Y.M.M. Antar, D. Roscoe and M. Cuhaci, “Recent Advances in Dielectric Resonator Antenna Technology,” IEEE Antennas and Propagation Magazine, Vol. 40, June 1998, pp. 35–48.
3. K.M. Luk and K.W. Leung, Eds., Dielectric Resonator Antennas, Research Studies Press, 2003.
4. A. Petosa, R. Larose, A. Ittipiboon and M. Cuhaci, “Microstrip-fed Array of Multi-segment Dielectric Resonator Antennas,” IEE Proceedings — Microwaves, Antennas and Propagation, Vol. 144, No. 6, December 1997, pp. 472–476.
5. A. Petosa, R. Larose, A. Ittipiboon and M. Cuhaci, “Active Phased Array of Dielectric Resonator Antennas,” IEEE Proceedings of the Antenna and Propagation Society, 1997, Montreal, Canada, pp. 690–693.
6. A. Petosa, A. Ittipiboon and S. Thirakoune, “Perforated Dielectric Resonator Antennas,” IEE Electronics Letters, Vol. 38, No. 24, November 2002, pp. 1493–1495.
7. A.A. Kishk, A.W. Glisson and G.P. Junker, “Study of Broadband Dielectric Resonator Antennas,” 1999 Antenna Applications Symposium, September 1999, Allerton Park, Monticello, IL, pp. 45–68.
8. R.K. Mongia and A. Ittipiboon, “Theoretical and Experimental Investigations on Rectangular Dielectric Resonator Antennas,” IEEE Transactions on Antennas & Propagation, Vol. 45, No. 9, September 1997, pp. 1348–1356.
Aldo Petosa received his B. Eng, M. Eng. and PhD degrees in electrical engineering from Carleton University, Ottawa, Canada, in 1989, 1991 and 1995, respectively. From 1990 to 1994, he carried out research on microstrip antennas for cellular and mobile satellite communication applications for CAL Corp., Ottawa, Canada. He joined the Communications Research Centre Canada in 1995, where he is presently the project leader in antenna design and development in the Advanced Antenna Technology Lab. He is currently working on various projects involving a wide range of antennas and arrays, including multi-layer microstrip antennas, dielectric lenses, dielectric resonator antennas and holographic antennas. He is also an adjunct professor with the department of electronics at Carleton University and teaches a graduate course in antennas.
Apisak Ittipiboon received his BE degree from Khonkaen University, Thailand, and his M.Sc. and PhD degrees in electrical engineering from the University of Manitoba, Winnipeg, Canada. Since 1985 he has been at the Communications Research Centre Canada, Ottawa, Canada, where he is currently a senior antenna research scientist and project leader. He is also an adjunct professor in the electrical and computer engineering department at the University of Manitoba. His current research includes low profile high gain leaky wave antennas, holographic antennas and applications of optical techniques for antenna designs. He has been involved in research and development work on dielectric resonator antennas, ultra wide band antennas and planar lenses. His interests include applied electromagnetics, waves on periodic structures, millimeter-wave technology and devices, and wireless communications.
